Question

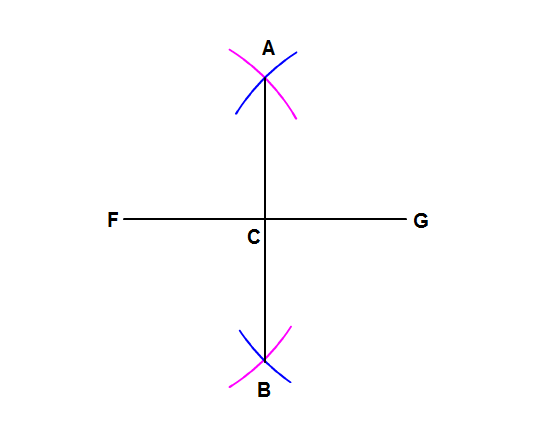
2. Using a straightedge and compass, construct the perpendicular bisector of FG? PLEASE HELP

Answer 1

Read my explanation below:
My drawings are NOT drawn to be accurate!
Also, I created these photos in Paint.

Explanation:

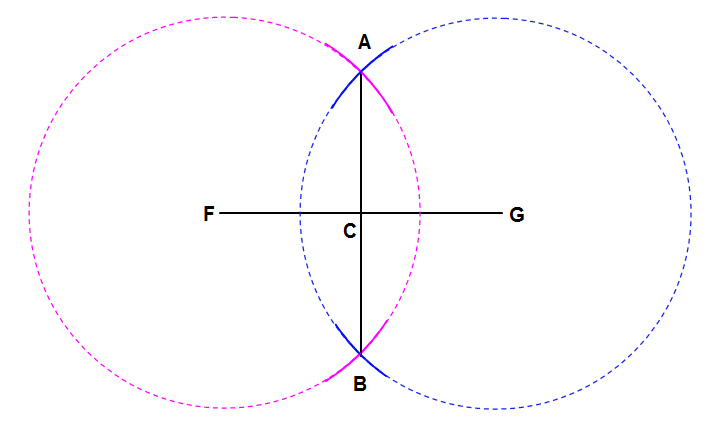
First, draw a circle with its center as point F. The radius of the circle is the length of the segment FG.

Now, draw a circle with its center as point G. The radius of the circle is the length of the segment FG.

Now, there will be two spots where the two circles F and G intersect. Connect these points with a straight edge.

Now you have the perpendicular bisector!

Answer 2

Steps

• The line segment `FG` is drawn by a straightedge. We are to draw perpendicular bisector of `FG`.
• The compass is so adjusted that it can be used to draw arc of radius greater than the half of the length of `FG`
• Now centering both F and G two arcs each on both sides of `FG` are drawn using compass.
• Let these four arcs intersect in pairs in two sides of `FG` at `A and B`
• `Aand B` are joined using sraight edge. The line `AB` intersects `FG` at C. This line `ACB` is the perpendicular bisector of `FG` at point C
• The figure will appear as shown below.