#2x^3-7x^2-2x+7#? How to factor it completely?
factor completely
factor completely
2 Answers
Explanation:
We take,
Explanation:
First, use trial and error to find an
Then you do a polynomial divsion of
(Don't know how to format this so I wrote it out and took a picture of it)
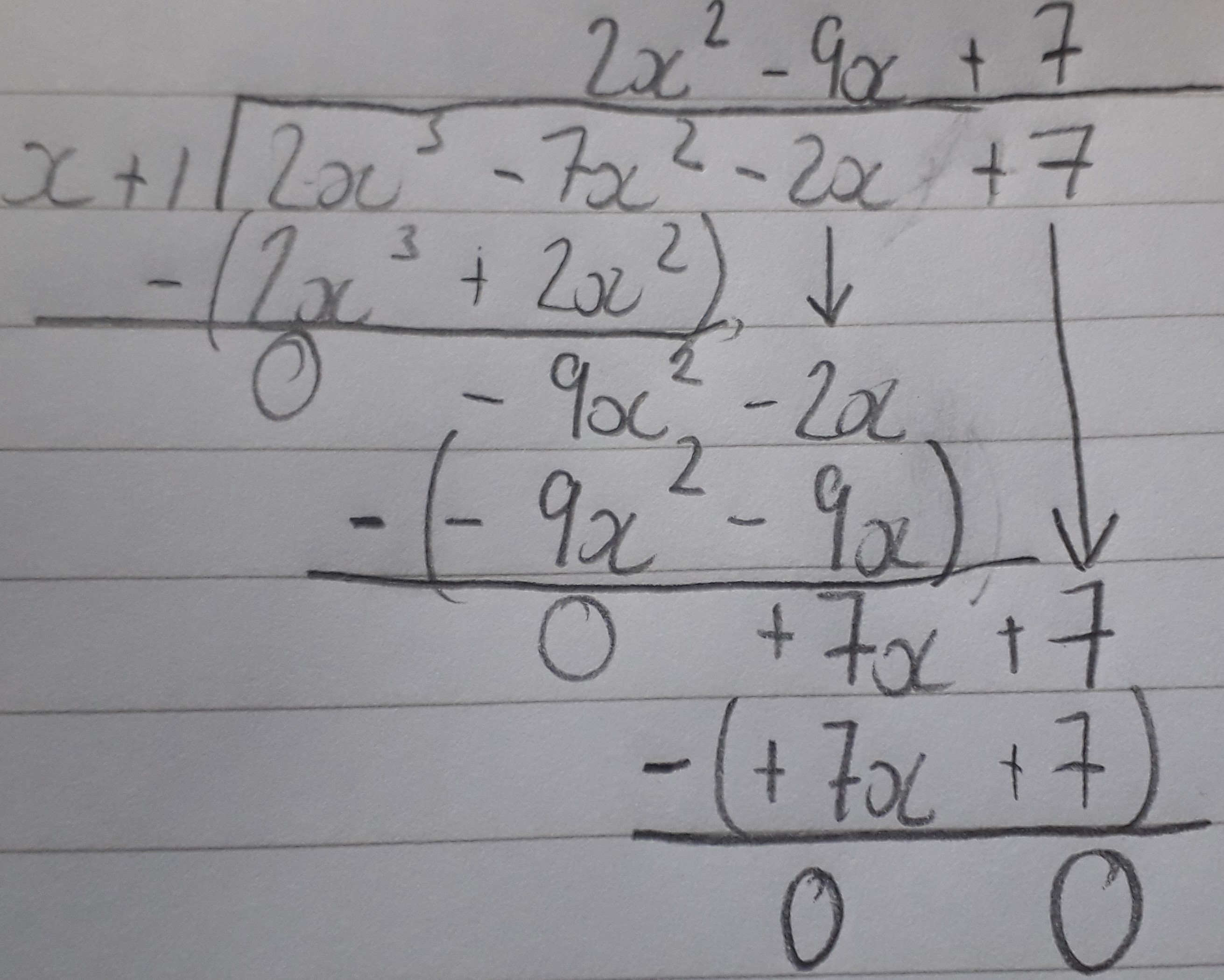
(The explaining of polynomial long division)
Now factorise the quadratic.
Which factors add up to nine and their product is 14? The factors are 2 and 7.
Then put the coefficient of


