30.60.90. right triangle. How do I solve if the long leg is 10?
I dont have the short leg or hypotenuse
I dont have the short leg or hypotenuse
1 Answer
May 1, 2018
The short leg is
Explanation:
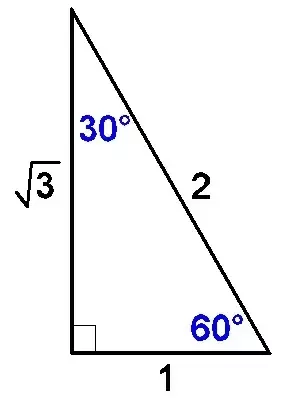
The 30.60.90 law states that for any given right triangle with angles measuring 30 and 60 degrees:
The 30 degree angle's opposite side is
The 60 degree angle's opposite side is
The 90 degree angle's opposite side is
 Quora
Quora
The "long leg" must be the 60 degree angle, so it is
The short leg is thus
Based on that, the hypotenuse is
We also need to rationalize the values.
