Electromagnetic radiation is made up of waves that are composed of photons which travel at the speed of light, #c#, in a vacuum, which is exactly 299,792,458 m/s, usually rounded to three significant figures as #"3.00"# x #"10"^(8)"m/s"#. Ask your instructor for his or her preference. All electromagnetic waves have wavelength and frequency.
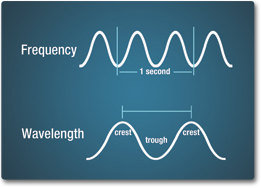
The wavelength is the distance between two crests, and is measured in length units, such as nanometers, centimeters, or meters. Wavelength is represented by the Greek lowercase letter lambda, #lambda#. Frequency is the number of crests that pass a given point within one second. One wave—or cycle—per second is called a Hertz (Hz). 1 Hz = 1/s or #"s"^(-1)#. Frequency is represented by the Greek lowercase letter nu, #nu#.
For any given photon of electromagnetic radiation, the wavelength times the frequency equals the speed of light: #c# = #lambda##nu#.
Example Problems
Problem 1. A photon of red light has a wavelength of #"4.50"# x #"10"^(-7)"m"#. Calculate its frequency.
Known/Given:
speed of light, #c# = #"3.00"# x #"10"^8"m/s"#
wavelength, #lambda# = #"4.50"# x #"10"^(-7)"m"#
Equation:
#c# = #lambda##nu#
Solution:
To solve for frequency, rearrange the equation so that
#nu# = #c#/#lambda#.
#nu# = (#"3.00"# x #"10"^8"m/s"#)#/#(#"4.50"# x #"10"^(-7)"m"#) = #"6.67"# x #"10"^14"/s"# = #"6.67"# x #"10"^14"Hz"#
The frequency of a photon of red light with wavelength #"4.50"# x #"10"^(-7)"m"# is #"6.67"# x #"10"^14"Hz"#.
Problem 2. A photon of green light has a frequency, #nu# of #"5.75"# x #"10"^14"Hz"#. What is its wavelength, #lambda#?
Known/Given:
speed of light, #c# = #"3.00"# x #"10"^8"m/s"#
frequency, #nu# = #"5.75"# x #"10"^14"Hz"# = #"5.75"# x #"10"^14"/s"#
Equation:
#c# = #lambda##nu#
Solution:
To solve for wavelength, #lambda#, rearrange the equation so that
#lambda# = #c#/#nu#.
#lambda# = (#"3.00"# x #"10"^8"m/s"#)#/#(#"5.75"# x #"10"^14"/s"#) = #"5.22"# x #"10"^(-7)"m"#
The wavelength of a photon of green light with frequency
#"5.75"# x #"10"^14"Hz"# is #"5.22"# x #"10"^(-7)"m"#.


