Question

Why is the ionization energy increasing for second and third-row transition metals, but constant for the first-row transition metals?

Answer 1

It's not. There are very clear, though nonstraightforward, nonzero changes across the transition metals. The ionization energies vary by between `"0.020 eV"` and about `"2.360 eV"` across the transition metals, which is definitely not constant.

However, the first-row transition metal ionization energies oscillate the most drastically, likely because their orbital energies are similar enough that small things like electron repulsion and electron shielding give rise to "exceptions" in a so-called trend.

Data from NIST shows:

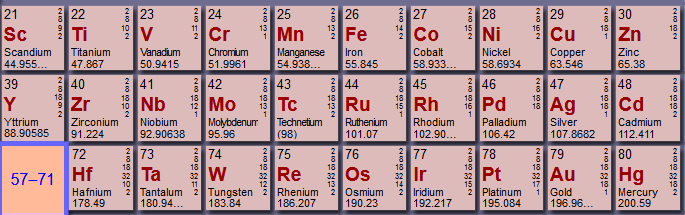
where, e.g. `"Ag"` is index `9` in the 2nd-row transition metals.

Consider the following observation (see indices `7` vs. `8`, `color(blue)"blue"` vs. `color(orange)"orange"`):

The first ionization energy of `"Ni"` (`3d^8 4s^2`) is lower than that of `"Co"` (`3d^7 4s^2`), whereas the first ionization energy of `"Pd"` (`4d^10 5s^0`) is higher than that of `"Rh"` (`4d^8 5s^1`).

Rh vs. Co (`r = "169 pm"` vs. `"152 pm"`)

Consider that `ul(overbrace("IE"_1("Rh"))^("7.459 eV") < overbrace("IE"_1("Co"))^("7.881 eV"))`.

One major factor is that the `5s` orbital is bigger than the `4s` orbital (sticks out from the nucleus more). Thus, it is easier to remove the `5s` electron from `"Rh"` and the contribution is to decrease `"IE"_1` of `"Rh"` relative to `"Co"`.

Further consider that `"Rh"` has a higher `ns` orbital potential energy than `"Co"` does (by about `"0.98 eV"`; see Appendix B.9), so its `5s` electron takes less energy to remove.

Lastly, `"Rh"` is also a bigger atom than `"Co"`, slightly decreasing the ionization energy further.

(This is actually a normal trend to expect.)

Rh vs. Pd (`r = "169 pm"` vs. `"173 pm"`)

Now consider the leap where `ul(overbrace("IE"_1("Pd"))^("8.337 eV") > overbrace("IE"_1("Rh"))^("7.459 eV"))`.
(This only seems like an abnormal IE trend at first, but it arose from an abnormal orbital potential energy trend, which we are not focusing on here.)

We accept that although `"Pd"` is slightly bigger than `"Rh"`, `"Pd"` has its `(n-1)d` orbitals filled, whereas `"Rh"` does not (it is beyond the scope of this answer to explain why).

As a result, one has to ionize `"Pd"` by removing a `bb(4d)` electron, which is significantly lower in energy than a hypothetical corresponding single `5s` electron (which would have required `"2.14 eV"` less energy to ionize than the `4d`).

Co vs. Ni (`r = "152 pm"` vs. `"149 pm"`)

And lastly, consider that `ul(overbrace("IE"_1("Co"))^("7.881 eV") > overbrace("IE"_1("Ni"))^("7.640 eV"))`.

This one is fairly simple. (It is not strictly due to the atomic radii, since `"Ni"` is smaller, which would contribute inversely to the trend.)

There is one more `3d` electron in `"Ni"` than in `"Co"`, which increases the electron shielding of the `4s` electrons by the `3d` electrons from the nucleus, and expanding the `4s` orbital radius of `"Ni"` relative to that of `"Co"`. This is evidently more significant than the difference in radii.

Thus, the first ionization energy of `"Ni"` is slightly lower.