Question #8aca8
2 Answers
Let's start by stating a couple of assumptions:
1. Water is generally incompressible.
2. The amount of water flowing through any cross-section of the stream will be the same at any height.
3. After coming out of the faucet, the water is influenced only by gravity.
Combining assumptions 1 and 2 we can say that the total flux of water
Assumption 3 allows us to describe the velocity at any height as a function of the initial velocity and the height.
A little algebra allows us to solve for the cross sectional area as a function of these variables:
The radius can be calculated from the area using the relation
The equation then becomes:
http://www-e.uni-magdeburg.de/mertens/teaching/seminar/themen/ajp_drop_formation.pdf
The cohesive force between water molecules binds them together as a liquid. Because of this we can assume that droplets of water are not breaking off from the main flow, so the shape of the water stream would pinch tighter and tighter as it fell. This would produce a horn shape.
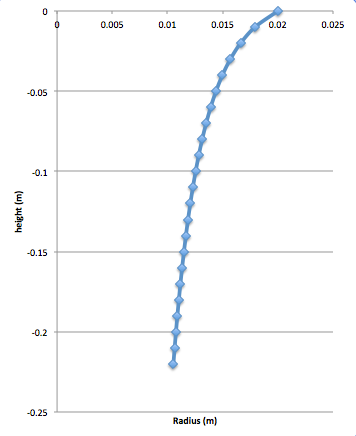
The mathematical shape would be a volume of rotation, where we would take a graph of the radius of the stream as a function of height and rotate it around the axis. To find this function, we'll start with the equation of continuity. If you have ever put your thumb over the end of a hose to make the water come out faster, you have demonstrated the equation of continuity;
Where
We can consider
which rearranges to;
Where
We can simplify this by setting
We can plug this into
A graph of
and if we rotate it around the x axis we get the shape of the water falling from a faucet. Accounting for the fact that the water actually has a starting velocity would move the graph to the left, making the slope shallower, and including the constants from



