Question

Question #517b1

Answer 1

This is an optimization problem, so lets start by setting up a function with one variable and taking a derivative. Then we can find any zeros of that derivative.

The problem states that we have 3 parallel partitions, so lets start with a basic drawing.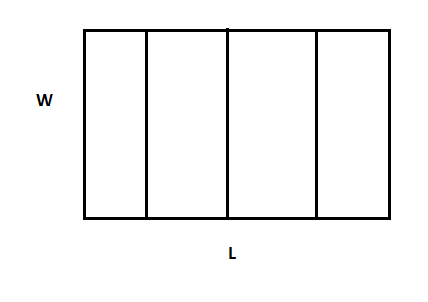
In the drawing above we have `5` equal sections of fence of length `W` and `2` equal sections of length `L`, all of which add up to `500ft` of fence. We can therefore set up the following equation:

`5W + 2L = 500`

Additionally, we are looking for the area, so we will need the formula for the area of a rectangle:

`A = L xx W`

Now we have two equations that we can combine to get one function to take the derivative of. Lets solve the first equation for `L`.

`2L = 500 - 5W`

`L = (500 - 5W)/2`

Now we can replace `L` in equation 2 with this equation to get a function for `A` in terms of `W`.

`A(W) = W((500 - 5W)/2)`

To make the derivative easier, lets make this a polynomial.

`A(W) = -(5W^2) /2 + (500W)/2`

We are looking for the extrema, which occur at turning points or where the derivative is equal to 0. Lets use the power rule to get the derivative and set it equal to 0.

`del/(delW) A(W) = -5 W + 500/2 = 0`

Solve for `W`.

`5W = 500/2`

`W = 50`

Great, we now have the length of one side of our fence! Lets use it to solve for `L`, the other side. Plug our value for `W` into our first equation to get;

`5 (50) + 2L = 500`

Solve for `L`.

`250 + 2L = 500`

`2L = 250`

`L = 125`

Now we have the dimensions for our fence. The largest possible pen would have a length of `125ft`. and a width of `50ft`. for a total area of `6250ft^2`.