Start with a drawing of the two graphs, just to get an idea of what we are looking at. I made this image using Geogebra and we have both graphs and a rectangle inscribed inside.
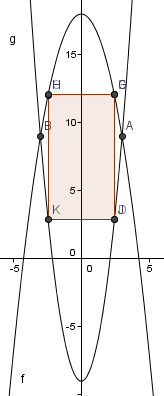
Now we need to think about what information we know has to be true about the rectangle. We know that for each function there is no #x#-coordinate that shares 2 #y#-coordinates. Therefore, the length of the vertical side of the rectangle is the distance between the two functions. Let's call this #L#.
#L = f(x) - g(x)#
We also know that we have two of these sides at two different #x# values. Lets call those positions #x_1# and #x_2# where #x_1# is left of the #y# axis and #x_2# is right, so that our two #L#s are;
#L_1 = f(x_1) - g(x_1)#
#L_2 = f(x_2) - g(x_2)#
It can also be shown that there is no #y# value inside the graphs that intersects both graphs. In other words, the other sides, #W#,each intersect one function twice. We can write this as;
#W_1 = W_2 = x_2-x_1#
But #f# and #g# are symmetric across the #y# axis, so #x_1 = -x_2# so;
#W = -x_1 - x_1 = -2x_1 #
Now lets plug #L_1# and #W# into the area equation.
#A = L xx W = (f(x_1) - g(x_1)) xx (-2x_1)#
Plugging in #f(x)# and #g(x)#;
#A(x)=((18-x^2) - (2x^2-9)) xx (-2x)#
#A(x) = -2x(27 - 3x^2)#
#A(x) = 6x^3 - 54x#
To optimize this function, we need to take the derivative and find the zeros. Using the power rule;
#del/(del x)A(x) = 18x^2 - 54 = 0#
#x^2 = 3#
#x = +- sqrt(3)#
The negative value is #x_1#, so lets plug this into our area function.
#A(-sqrt(3)) = 6(-sqrt(3))^3 - 54(-sqrt(3))#
# = 54sqrt(3) - 18sqrt(3)#
# = 36sqrt(3)#
This is roughly equal to 62.35.

