Question #631ca
1 Answer
Cobalt(II) (cobaltous) is considered to be more stable than cobalt(III) (cobaltic).
The electron configuration of cobalt is
The 4s electrons are highest in energy and are the valence electrons therefore Co(II) is
In general the relative stability of the +2 state is greater with respect to the +3 as we cross the 1st transition series. However it must be stated that stabilities vary a great deal with the chemical environment - temperature, physical state, solvent, pH, type of ligand etc.
If we consider the Co(III)/Co(II) redox potential:
This shows that Co(III) is quite strongly oxidising favouring formation of Co(II). It will even oxidise water.
The +3 state can, however, be greatly stabilised by complexing with a ligand such as ammonia.
Here we can see that the redox potential is much less +ve and now the stability of the Co(III) is greatly improved.
To explain this we need to look at how the ligands affect the 3d sub-level. In octahedral symmetry the central metal ion is surrounded by 6 ligands.

In the gaseous ion the 3d orbitals are said to be degenerate which means of equal energy.
However when surrounded by 6 ligands, 2 of the 3d orbitals are destabilised while 3 are stabilised. This is due to the particular shape of the d orbitals which I won't go into here. This is shown in the diagram.
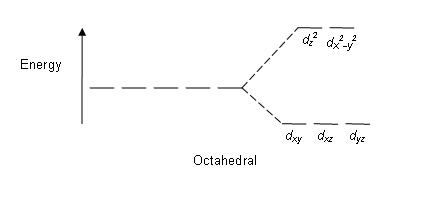
Co(III) is
The size of this energy gap is affected by the nature of the ligand.
This relative instability of uncomplexed Co(III) is reflected in the rarity of simple salts whereas Co(II) salts are very common.

