Question #404a8
1 Answer
I assume you want to know how to go from 1 length unit to another using exponents.
The units system is based on powers of 10. Since you want to know about size in meters, it's useful to look at metric prefixes, which are unit prefixes that come before a basic unit of measure to indicate a decadic (just means base ten) multiple or fraction of the unit.
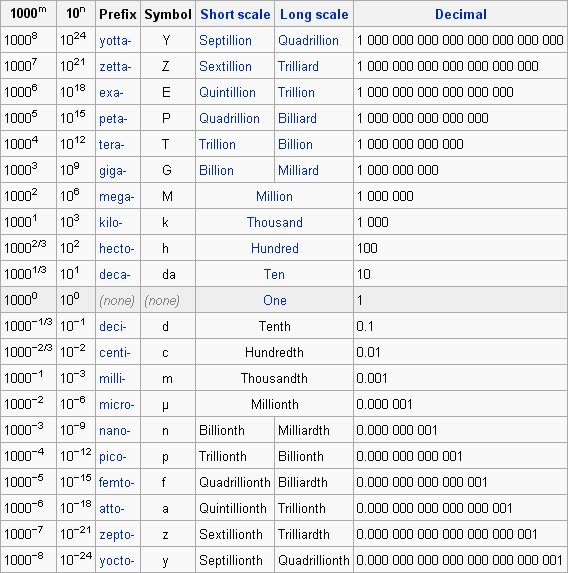
So, if you have a length of 800 meters, or 800 hectometers, what that means is that you have
One meter is expressed as
Let's say you want to go from 12.5 kilometers to 12.5 nanometers. Since 1 kilometer has 1000 meters, you can write
One nanometer is one billion times smaller than a meter, so you could say
Therefore,
So, for relative sizes, convert whatever units you have to meters and then use the unit prefixes to express the particular value you have. You can play around with expressing various numbers as powers of 10; after a while, this will become second nature and you'll be able to go from one unit to another with very little effort

