Question

Question #cd107

Answer 1

Let's first draw a triangle to get the trigonometry right.

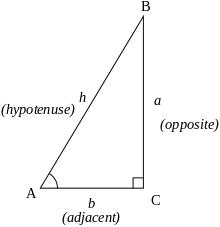
We'll use `angleA` instead of `x` because of the picture

`cosA` is defined as `b//h`
`tanA` is defined as `a//b`

So we get: `cosA*tanA=cancelb/h * a/cancelb=a/h`

Which is the definition of the sine .

Answer :
`cosA*tanA=sinA`

Extra
You could have done this another way if you knew that

`tanA=sinA/cosA`

Then it would be:

`cosA*tanA=cancel(cosA)*sinA/cancel(cosA)=sinA` (same result)

(picture: Wikipedia)

Answer 2

`cosx tanx -= sinx`

Explanation:

`cosx tanx -= cosx * sinx/cosx -= sinx`