What is meant by the "base" and "exponent" of a number and how do these relate to logarithms?

1 Answer
Alan P.
Mar 2, 2015

Exponentiation:
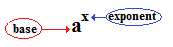
enter image source here
Base Definition:
( for integer exponent values greater than or equal to zero )

#a^x = 1# multiplied by #a#, #x# times

example:
#3^5 = 1 xx 3 xx 3 xx 3 xx 3 xx 3#
(#=243, if you're keeping track)

Note: based on this definition #a^0 = 1# for any value of #a#.

Important Insight:
#a^x xx a^y #
#= (1 xx a# (x times)#) xx (1 xx a# (y times)#)#
#= (1 xx a# (x+y times)#)#
#= a^(x+y)#

This insight is used to extend the definition of exponentiation to include negative and fractional exponents

#a^(-x) = 1/(a^x)#

#a^(1/x) = x^(th)# root of #a# (sorry; I don't know how to get the symbols for this)

Also
#(a^x)/(a^y) = a^(x-y)#
and
#(a^x)^y = (a^y)^x = a^(xy)#

Logarithms:
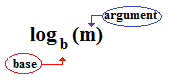
enter image source here
#log# with some specified base is a function.

Definition:
The value of #log_b(m) =# the value of #y# needed to make #b^y = m#
(Repeat that multiple times before going on. Come back to it as often as you need).

Example:
#log_3(81) = 4# since #3^4 = 81#

Common log identities:
#log_b(b) = 1#

#log_b(b^x) = x#

#log_b(c^x) = x log_b(c)#

#log_b(mn) = log_b(m) + log_b(n)#

#log_b(m/n) = log_b(m) - log_b(n)#

#log_b(m^n) = n log_b(m)#

Some special #log# notes:

  • Sometimes you may see #log (m)# written without a base specified; the convention in this case is that the base is #10#
  • Often you will see #ln(m)#; this is another form of the #log# function with a special base value, #e#; that is
    #ln(m) = log_e(m)#
    where #e# is a special number (like #pi#) approximately equal to #2.72#; #e# has some special properties that make it useful in calculus.
Related questions
Impact of this question
881 views around the world
You can reuse this answer
Creative Commons License