Question #b2b2b
2 Answers
This is a very simple problem if you're familiar with the Born-Lande equation for calculating lattice energies. Here's how that looks like
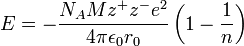
I won't list what all the terms in this equation mean because all but three of them are not important. The three terms that you should focus on are
Now, I believe that you are supposed to ignore the terms that are specific to individual ionic compounds, and assume that all the constants for your hypothetical salt are identical to those for
If that's the case, you can rewrite the above equation like this
Now, because
In the case of
Since
Rounded to three sig figs, the answer will be
The lattice energy of
If we consider 2 charges
So
We can find the work done in separating these charges from a distance
From which we get:
This means that if we double the charges the work done required to separate them would go up by 2 x 2 = 4.
This means that in your example the lattice energy would increase to 4 x -744 =
In this answer I have only considered 2 charges separated by a distance
A more accurate expression for lattice enthalpy
I won't go further into the details of this. If you want you can look up "Madelung Constant".


