Question #95b54
2 Answers
Sodium fluoride,
Sodium fluoride and magnesium oxide are actually isosteric compounds, i.e. they have the same number of valence electrons, but they differ in the type of atoms that form them.
Because the cations and anions that form these two compounds differ by just 1 unit of charge (
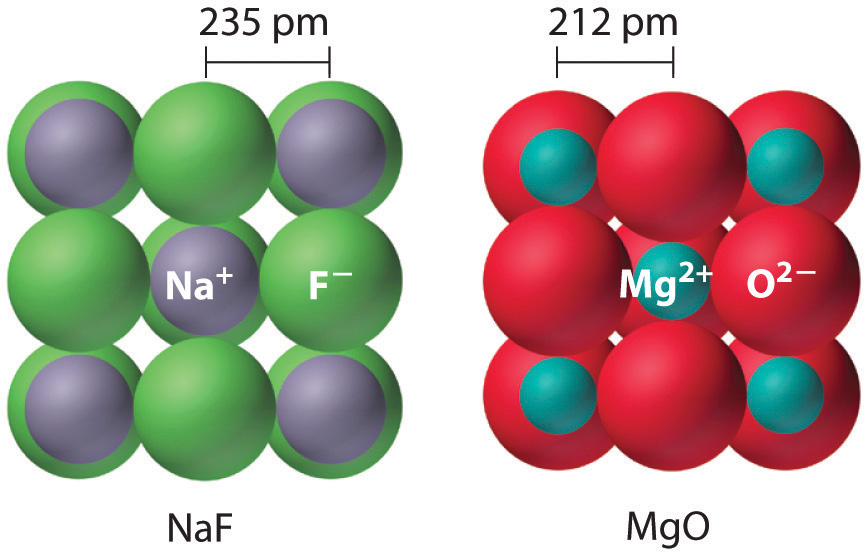
As you can see, the interionic distances are shorter in the case of
They are isomorphous because the ratio of the radii of their cations and anions
Ionic bonds are non - directional and an ionic solid will consist of a symmetrical array of positive and negative ions.
They will form a structure that ensures a minimum amount of energy, hence maximum stability.
If cations are equal in size to anions each cation would touch 12 anions and vice versa. The coordination number is said to be 12.
In reality cations tend to be smaller than anions so it is not possible to "fit" 12 anions around them so coordination numbers tend to be less than 12.
It is the ratio of the cation to anion radius
By doing some geometry (which I won't go into here) it can be shown that if
For
For
So
Since this lies within the range stated it forms this structure:
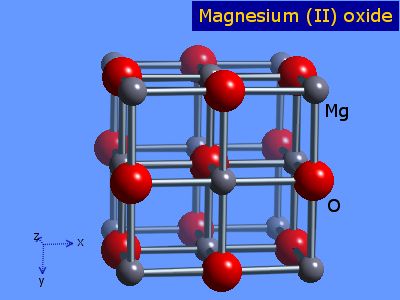
The "bonds" are actually points of contact. If you look at the
There is an ion at the centre of the face of the cube, so this structure is referred to as "face - centred cubic".
For
Since this value is between 0.414 and 0.732 we can also predict a face - centred cubic structure.


