Question

Question #fe76a

Answer 1

The slope represents `K_"m"/V_("max")`.

The starting curve for your double reciprocal plot is actually the Michaelis-Menten Plot, which looks like this

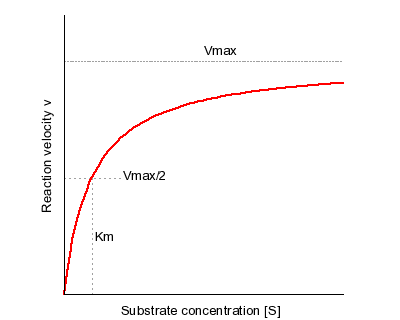
The above plot shows the rate of an enzyme-catalyzed reaction, `V`, as a function of the substrate concentration, `[S]`.

The equation plotted looks like this

`V = (V_("max") * [S])/(K_m + [S])`, where

`V_("max")` - the maximum rate of the reaction;
`K_m` - the substrate concentration when the rate is equal to `V_("max")/2`.

Now, you need to get from `V` and `[S]` to `1/V` and `1/([S])`, so just use the multiplicative inverse of the above equation to get

`1/V = (K_m + [S])/(V_("max") * [S])`

`1/V = K_m/(V_("max") * [S]) + cancel([S])/(cancel([S]) * V_("max"))`

`1/V = K_m/(V_("max") * [S]) + 1/V_("max")`

Now, to get to slope, think of the `y = mx + b" "` equation for a line

`underbrace(1/V)_("y") = underbrace(K_m/V_("max"))_(color(red)(m)) * underbrace(1/([S]))_text(x) + underbrace(1/(V_max))_(b)`

This plot is called the Lineweaver-Burk plot and it looks like this

Answer 2

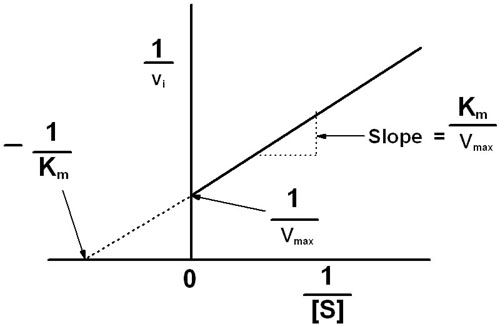
The slope is equal to `K_"m""/"V_"max"`.

A double reciprocal plot is used for analyzing enzyme kinetics.

It is a useful method for analyzing the Michaelis-Menten equation:

`V = (V_"max"[S])/(K_"m" + [S])`

where `V` is the reaction velocity, `V_"max"` is the maximum reaction velocity, `[S]` is the substrate concentration, and `K_"m"` is the Michaelis-Menten constant.

Taking the reciprocal gives

`1/V = (K_"m" + [S])/(V_"max"[S]) = K_"m"/V_"max" 1/([S]) + 1/V_"max"`

The equation is of the form `y = mx + b`

where `y = 1/V`, `m = K_"m"/V_"max"`, `x = 1/([S])`, and `b = 1/V_"max"`.

A plot of `y` vs `x` or `1/V` vs `1/([S])` is called a double reciprocal plot or a Lineweaver-Burk plot.

The `x`-intercept is `-1/K_"m"`.

The `y`-intercept `b = 1/V_"max"`.

And the slope `m = K_"m"/V_"max"`.