The key to solving this problem is to realize that an uncompetitive inhibitor does not change the slope of the double-reciprocal plot that describes the enzyme-catalyzed reaction when no inhibitor is present.
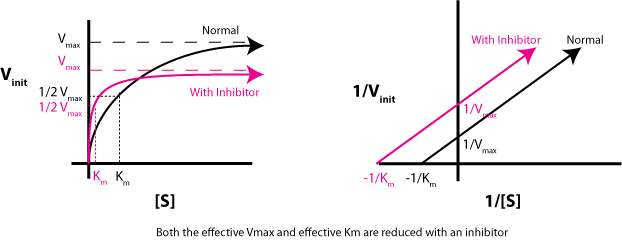
This is important because, for an uncompetitive inhibition, both #V_"max"# and #K_m# decrease by the same factor, which is why the slope remains unchanged.
More specifically, both #V_"max"# and #K_m"# decrease by
#1 + ([I])/K_I^(')#, where
#[I]# - the concentration of the inhibitor;
#K_i^(')# - the inhibitory constant.
However, this is actually equal to #alpha^(')#, the degree of inhibition.
As a result, #V_"max"^(')# will be equal to
#V_"max"^(') = V_"max"/(1 + ([I])/K_I^(')) = V_"max"/(alpha^('))#
Therefore,
#V_"max" = alpha^(') * V_"max"^(') = 3.00 * "9.00 nmol s"^(-1) = "27.0 nmol s"^(-1)#
SIDE NOTE Check out this great site on enzyme inhibition, it allows you to play with Lineweaver-Buk plots for various inhibitors
http://higheredbcs.wiley.com/legacy/college/voet/0470129301/guided_exp/guided_exploration_11/michaelis_menten.html


