What does a mixed inhibitor (as opposed to a competitive or non/uncompetitive inhibitor) do to the slope and y-intercept of a Lineweaver-Burk, or Double-Reciprocal plot?
1 Answer
A mixed inhibitor changes both the slope and the y-intercept of a double-reciprocal plot.
In this case, you have to look at the equation that describes the Lineweaver-Burk plot for all the cases mentioned and figure out which one corresponds to the given criteria.
When no inhibitor is present, the Lineweaver-Burk equation looks like this
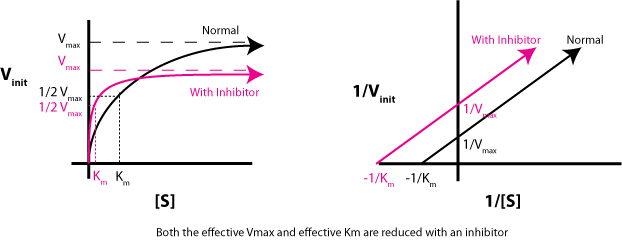
Now, when an uncompetitive inhibitor is present, the Lineweaver-Burk equation becomes
As you can see, the y-intercept changes, i.e. it goes up by a factor of
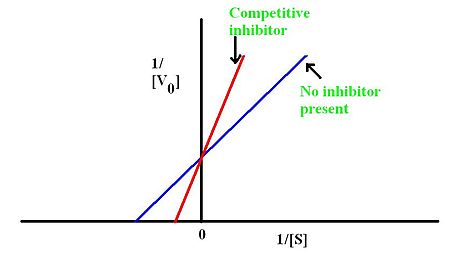
When a competitive inhibitor is present, the Linewaver-Burk equation becomes
This time, the slope of the line changes by a factor of
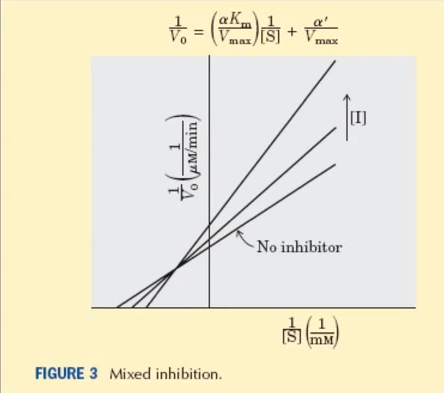
Finally, when a mixed inhibitor* is present, the equation becomes
Now both the slope and the y-intercept change, the former by a factor of
SIDE NOTE The terms

