Question #d3c9f
1 Answer
Apr 10, 2015
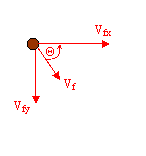
First divide the initial velocity vector into horizontal components and vertical components.
The horizontal component will be
I am assuming we are neglecting air resistance so this value will remain constant.
The vertical component will be
Now combine the two components to get the final velocity