Question #bfe91
1 Answer
So, you need to prepare a certain volume of a solution that has a certain molarity.
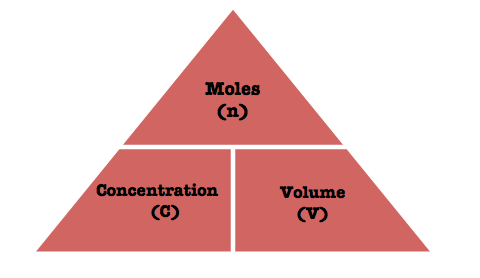
Molarity expresses the number of moles of solute, which you have to determine, dissolved per liter of solution.
If you have 1 mole of a solute dissolved in 1 L of solution, you'll have a 1 M solution
Since you know the volume and the molarity, you can rearrange the equation to solve for the number of moles that would give you that respective molarity
For the above example, if you are given 1 L of a 1-M solution, the number of moles of solute will be
 https://shirleycahyadi.wordpress.com/category/uncategorized/
https://shirleycahyadi.wordpress.com/category/uncategorized/
Keep in mind that you must always use liters for the volume; even if you are given the volume in mililiters, you must convert it to liters when applying the molarity equation.
Here's another example. Let's say I give you 100 mL of a 1-M solution and ask you to determine the number of moles of solute present.
You'd get
Compare this with the 1-L, 1-M solution. The volume is now 10 times smaller, but the molarity is the same, which means that you must have 10 times fewer moles present.
If you add 1 mole to 100 mL, the molarity will be 10 times greater than when you had 1 mole in 1 L because you get the same amount of moles in a smaller volume

