Question #7c91f
1 Answer
May 16, 2015
My guess would be
By obstructed I am assuming the pendulum bob is on a string that hits a peg or other obstruction at the halfway point of its swing (see diagram)

I'm not 100% sure but believe the period of this type of pendulum will be the average of the period on the unobstructed side
The relationship between period and length is given as
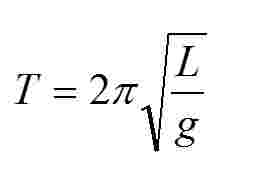
So for
The mean value of the two periods (and the period of the obstructed pendulum) would be equal to

