Question

What is the electron configuration of `"Pt"^(2+)"`, according to the Madelung rule?

Answer 1

The electron configuration of `"Pt"^(2+)"` is `[Xe]4f^(14)5d^(8)`.

---

The energy of an electron in an atom increases with increasing value of `n` the principal quantum number.

Within an energy level, as defined by `n`, there are sub - levels which are defined by the angular momentum quantum number `l` which takes integral values of zero up to `(n-1)`

The sub - levels in order of increasing energy (for the same `n`) are `s < p < d < f`, etc.

The Madelung Rule states that the energy of an electron depends on the value of `(n+l)`. This gives us the so - called "Aufbau Principle" and the energy level diagram you see in text - books:

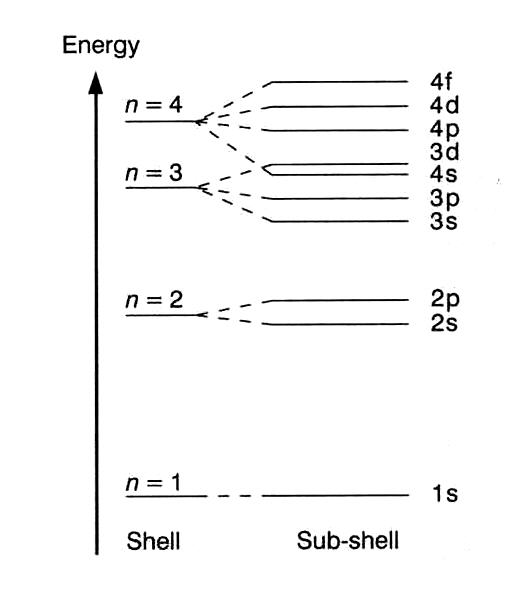
You can see that in the diagram, the `4s` is lower in energy than `3d`, so it typically fills first:

For `4s` we get `(n+l)=4+0=4`

For `3d` we get `(n+l)=3+2=5` i.e higher in energy.

The problem lies in the fact that this diagram does not apply to all atoms nor should we expect it to.

After calcium the rule starts to break down as complex electron interactions take place. These become especially significant as the electron energy levels get closer and closer together for bigger atoms.

For the first transition series the `3d` drops in energy relative to the `4s` (different texts give different results when this exactly happens). This effectively means the `4s` is somewhat higher in energy and these electrons are lost first and define the atomic radius of the atom.

Again, as just mentioned, the 4s-3d interactions are more complex than at first glance.

For instance, they are why iron (`"Fe"^(0)`) is `[Ar]3d^(6)4s^(2)` and not `[Ar]3d^(8)4s^(0)`, even though the `3d` starts getting filled first.

Let's apply the Madelung Rule to the examples in your question:

`[Xe]6s^(2)4f^(14)5d^(8)`

For `6s` we get `(n+l)=6+0=6`

For `4f` we get `(n+l)=4+3=7`

For `5d^(8)` we get `5+2=7`

When 2 sub - shells have the same value of `(n+l)` i.e `7` the one with the highest `n` value is said to be higher in energy.

So the Madelung Rule/Aufbau principle would predict that configuration. You can apply that reasoning to `[Xe]4f^(14)5d^(10)`in which both sub - shells have `(n+l)` values of `7`

The correct configuration according to "Cotton and Wilkinson" is:

`color(green)([Xe]4f^(14)5d^(9)6s^(1))`

This is not in accordance with the Madelung Rule/Aufbau Principle for the reasons already stated.

So losing the `6s` and one from `5d` gives `"Pt"^(2+)"`:

`color(blue)([Xe]4f^(14)5d^(8))`

The Madelung Rule is a rule and not a law so is not applicable in all cases.