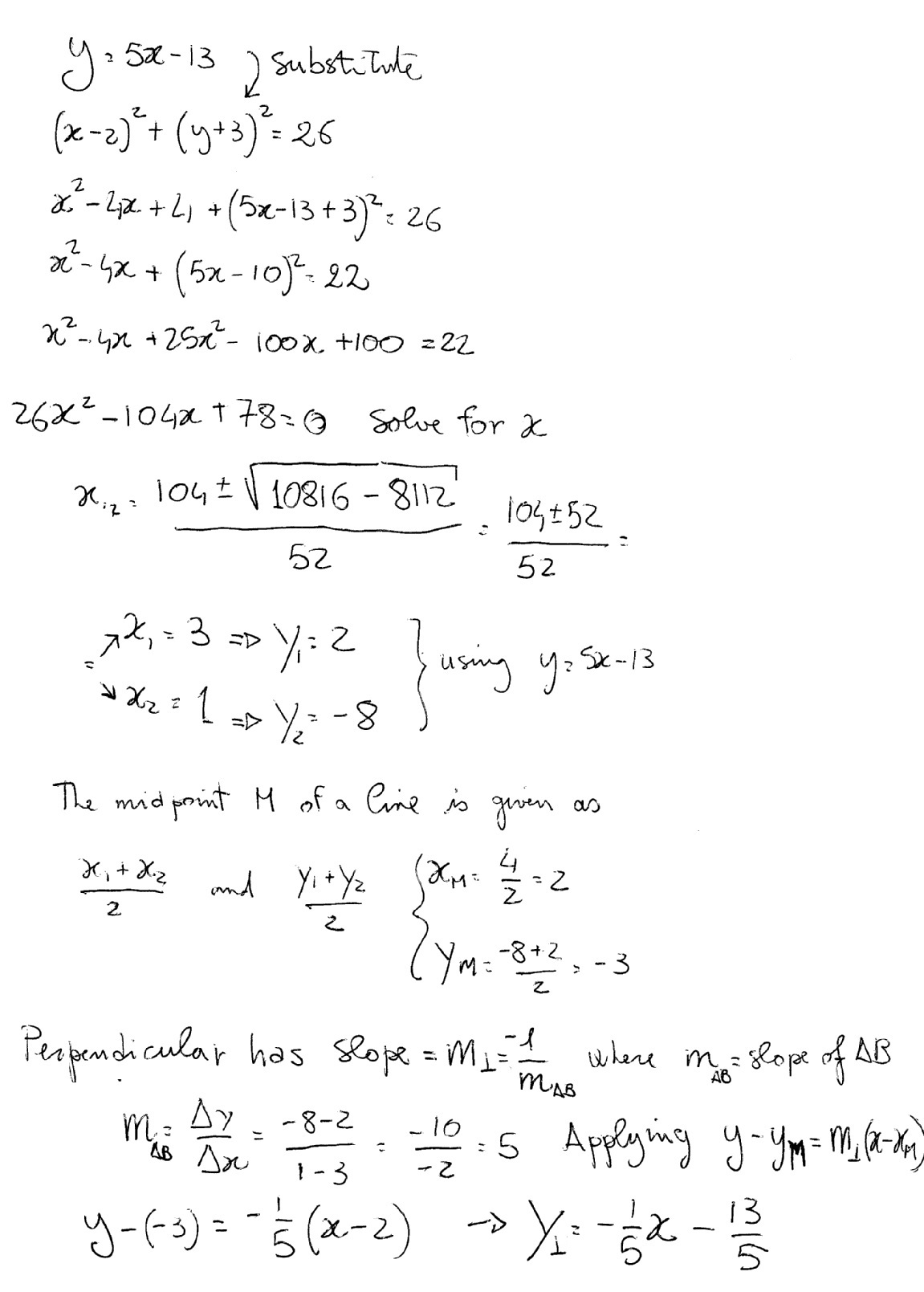Line:
#y = 5*x - 13#
Circle:
#(x-2)^2 + (y+3)^2 = 26#
If we want the intersection points, we substitute the line #y# in the Circle equation:
#(x-2)^2 + ((5*x - 13)+3)^2 = 26#
#(x-2)^2 + (5*x - 10)^2 = 26#
#(x-2)^2 + (5*(x - 2))^2 = 26#
#(x-2)^2 + 25*(x - 2)^2 = 26#
#26*(x-2)^2 = 26#
#(x-2)^2 = 1#
#x^2 - 4*x + 3 = 0#
#x_1 = 1#
#x_2 = 3#
#y_1 = 5*x_1 - 13 = -8 -> A = (1,-8)#
#y_2 = 5*x_2 - 13 = 2 -> B = (3,2)#
Finding #M#:
If #M# is the midpoint of #AB#,
#vec M = (vec A + vec B)/2#
#vec M = [1+3, -8+2]*1/2 = [2,-3]#
#M = (2,-3)#
Perpendicular line #y = m*x+c# :
As shown in
https://www.mathsisfun.com/algebra/line-parallel-perpendicular.html,
#m = -0.2#
and #(P_0 = M)#
#(y-y_0) = m*(x-x_0)#
#(y-(-3)) = -0.2*(x-2)#
#y+3 = -0.2*x + 0.4#
#y = -2.6 - 0.2*x# is the equation of the perpendicular line to #AB# that crosses it in #M#.
Hope it helps