Question #8e66d

Question

1352 views around the world

You can reuse this answer
Creative Commons License

Answer 1 · 2015-05-27T11:12:33

#sin^2 + cos^2 = 1#

#sin^2 + cos^2 = 1#

This is one of the basic relationships based on the Pythagorean Theorem.

For a triangle with legs #x# and #y#, and a hypotenuse of #r#

By the Pythagorean Theorem: #x^2+y^2 = r^2#

By definition of sin and cos
#sin = y/r#
#cos = x/r#
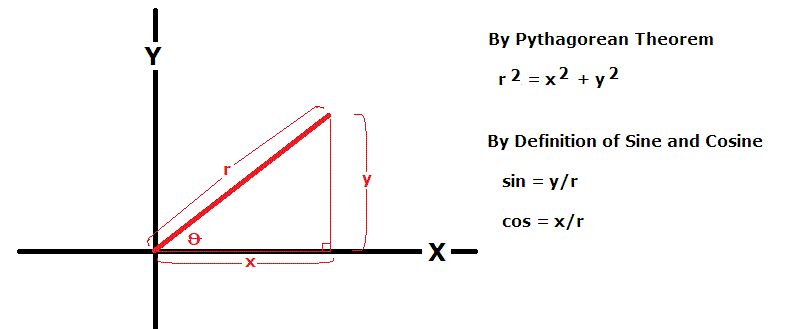
enter image source here
So #sin^2 + cos^2#

#=(y/r)^2 +(x/r)^2#

#=y^2/r^2 + x^2/r^2#

#= (y^2+x^2)/r^2#

#= r^2/r^2#

#=1#

Answer 2 · 2015-09-09T09:52:50

We dont know if it is the same argument in the equation given.Of course for a given x we have that #sin^2x+cos^2x=1#