Question

Question #7ab5e

Answer 1

After six hours, the box will contain 3.7 kg of ice.

Here's what the idea behind this problem is. Since the problem provided the enthalpy of fusion of ice, you know that the temperature inside the box is `0^@"C"`.

Because the outside of the box is at a higher temperature, heat will flow from the room and into the box via conduction. This will cause the ice to undergo a phase change, i.e. a certain amount of ice will melt.

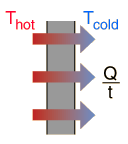
This means that the heat that flows into the box will be equal to the heat absorbed by ice.

`Q_"room" = q_"ice"`

The heat transferred by conduction can be written like this

`Q/t = (k * A * DeltaT)/d`, where

`Q` - the amount of heat;
`t` - the time that passed, in your case 6 h;
`k` - the thermal conductivity of the material, in your case `"0.01 J/s"^(-1)"m"^(-1)""K"^(-1)`
`A` - the cross sectional area of the box;
`DeltaT` - the difference between the higher temperature and the lower temperature;
`d` - the thickness of box.

Since you'r edealing with a cubic box, the total area will be

`A = 6 * "0.3 m"^2 = "0.54 m"^2`

Plug your values into this equation to determine how much heat flows into the box in six hours, but keep in mind that you need to convert hours to seconds and centimeters to meters.

`6cancel("hours") * (60 cancel("minutes"))/(1cancel("hour")) * "60 seconds"/(1cancel("minute")) = "21600 s"`

`Q/(21600cancel("s")) = ("0.01 J" cancel("s"^(-1)) cancel("m"^(-1)) cancel("K"^(-1)) * 0.54cancel("m"^2) * (30-0)cancel("K"))/(0.03cancel("m"))`

`Q = 21600 * ("0.01 J" * 0.54 * 30)/0.03 = "116640 J"`

Since this will be equal to the heat absorbed by the ice, you can use it to determine how much ice melted

`q_"ice" = m * H_"fus" = Q_"room"`

`Q_"room" = m * H_"fus" => m = Q_"room"/H_"fus"`

`m = (116640cancel("J"))/(335 * 10^3 cancel("J")/"kg") = "0.348 kg"`

This means that you'll be left with

`m_"unmelted" = m_"initial" - m`

`m_"unmelted" = 4 - 0.348 = 3.652 = color(green)("3.7 kg")`

SIDE NOTE I used two sig figs for the answer, despite the fact that your values require only one sig fig.

In this case, using one sig fig would imply that all the ice remained unmelted.