Question #7ab5e
1 Answer
After six hours, the box will contain 3.7 kg of ice.
Here's what the idea behind this problem is. Since the problem provided the enthalpy of fusion of ice, you know that the temperature inside the box is
Because the outside of the box is at a higher temperature, heat will flow from the room and into the box via conduction. This will cause the ice to undergo a phase change, i.e. a certain amount of ice will melt.
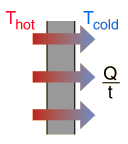
This means that the heat that flows into the box will be equal to the heat absorbed by ice.
The heat transferred by conduction can be written like this
Since you'r edealing with a cubic box, the total area will be
Plug your values into this equation to determine how much heat flows into the box in six hours, but keep in mind that you need to convert hours to seconds and centimeters to meters.
Since this will be equal to the heat absorbed by the ice, you can use it to determine how much ice melted
This means that you'll be left with
SIDE NOTE I used two sig figs for the answer, despite the fact that your values require only one sig fig.
In this case, using one sig fig would imply that all the ice remained unmelted.

