Question #06856
1 Answer
The probability to that both balls have odd numbers is
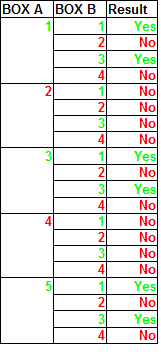
There are 5 balls in the box A, numbered 1 2 3 4 5, and there are 4 balls in the box B, numbered 1 2 3 4.
You take one ball from box A and one ball from box B.
In other words, for every ball you take from box A, you take one ball from box B.
That gives you a total of
Among the five balls in the box A, three have an odd number and two have an even number.
Among the four balls in box B, two have an odd number and two have an even number.
Therefore, there is a total of
The probability of an event to happen is calculated as
(number of favorable outcomes)/(number of possible outcomes)
Here, that is
And since a good picture is worth a thousand words: