#z^alpha/{z^n+1}# has simple poles at
#z_k=exp(ipi(1/n+{2k}/n), \quad \quad k=0, 1, 2, ...\quad (n-1)#
Note that #d/dz[z^n+1]=nz^{n-1}# is analytic for #n>1# and is not zero at #z_k#. Therefore, #z_k# is a zero of order 1 of #(z^n+1)# which lets us write:
#(z^n+1)=(z-z_k)g(z)#
where #g(z)# is analytic and #g(z_k)\ne 0#. It follows that
#z^alpha/{z^n+1}= { z^alpha/g(z)}/{(z-z_k)}#
The residue at #z_k# is
#B_k=(z_k)^alpha/g(z_k)#
To find #g(z_k)# use,
#d/dz[z^n+1]=d/dz[(z-z_k)g(z)]#
#nz^{n-1}=g(z)+(z-z_k)g'(z)#
Sub #z=z_k \quad \implies \quad g(z_k)=n(z_k)^{n-1}#
#\implies \quad B_k=(z_k)^alpha/{n(z_k)^{n-1}}=1/n(z_k)^{1+alpha-n}#
Now we must choose an integration path. The problem is choosing a path that won't have a singularity on it for any value of #n#. I am going to use the path described below.
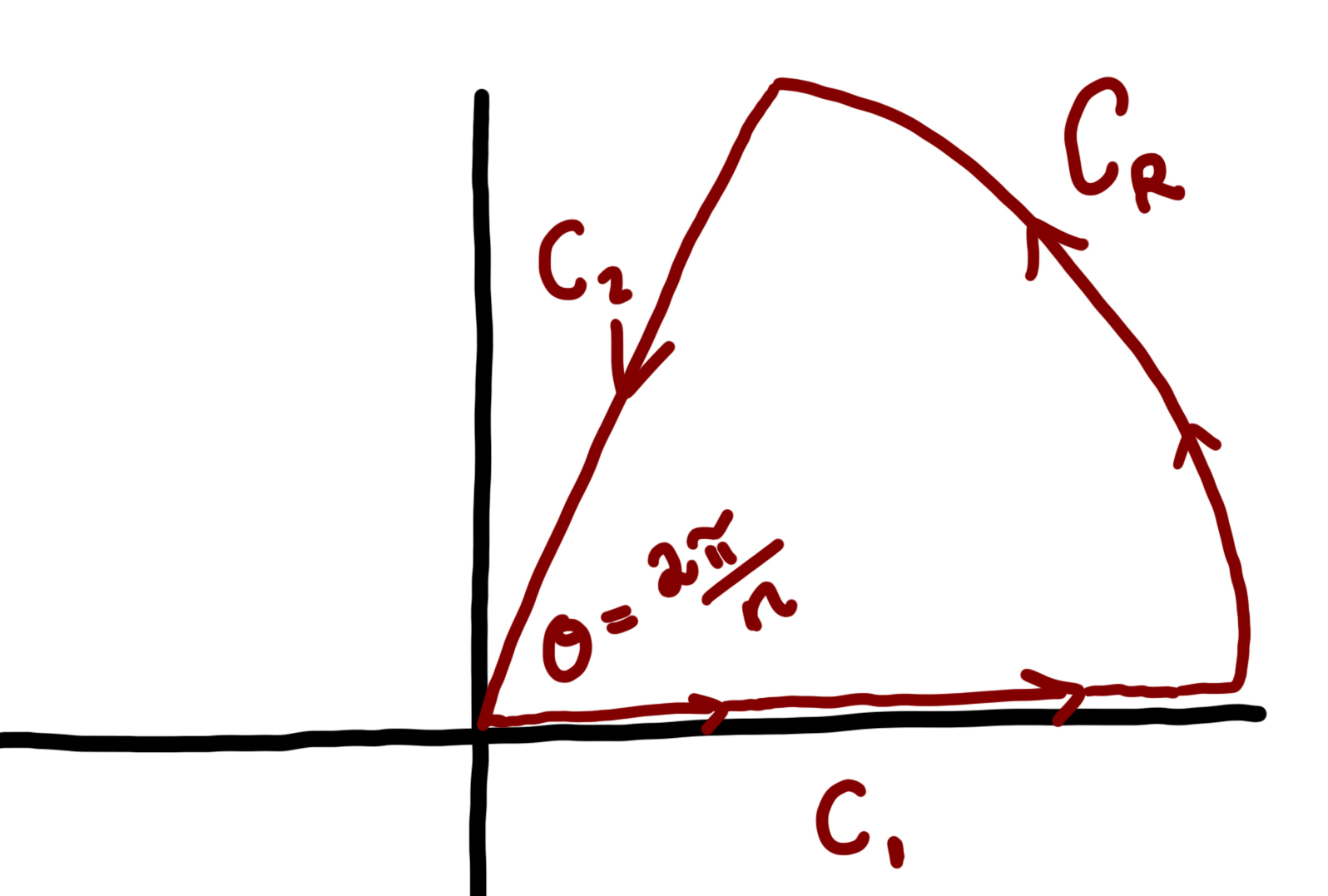
#C_1=int_0^inftyx^alpha/(x^n+1)dx#
#C_2=int_infty^0(Re^{i{2pi}/n})^alpha/((Re^{i{2pi}/n})^n+1)dR=e^{i2pialpha/n} int_infty^0 R^alpha/(R^n+1)dR#
Note that
#C_2=-e^{i2pialpha/n}C_1#
Before evaluating #C_R# consider
#|z^alpha/(z^n+1)| leq R^alpha/{R^n-1}#
So #|C_R| \leq R^alpha/{R^n-1} 2pi R=2pi 1/{{(R)^{n-(alpha+1)}}-R^{-alpha-1}}#
We are given that #n>(alpha+1)#, Therefore #lim_{R\rarr infty}C_R=0#
Note that I have chosen #theta# in the diagram so that only one singularity is enclosed. Therefore we only have to consider the first residue, #B_0#.
#C_1+C_2+C_R=2pi i B_0#
Substitute values and solve for #C_1#
#C_1(1-e^{i2pialpha/n})+0=2pii1/n(z_0)^{1+alpha-n}#
Sub #z_0# To get the answer:
#int_0^inftyx^alpha/(x^n+1)dx=C_1={2pii}/{n}1/(1-e^{i2pialpha/n})e^{ipi(1+alpha-n)/n}#

