If the sum of two unit vectors is a unit vector, what is the magnitude of the difference of the two vectors?
2 Answers
Unit vector: The vector whose magnitude is unity(1) is called unit vector.
Explanation:
Let ai+bj and ci+dj be the unit vectors.
From the defination,
Add the above two vectors,
(ai+bj)+(ci+dj) =(a+c)i+(b+d)j__(3)
Also given that,
The magnitude of equation(3) is also unity.
the magnitude of their difference is:?
THe difference of two unit vectors is
If the sum of two unit vectors is a unit vector, then the magnitude of their difference is 1.73205
The magnitude (length) of the difference is
(Alternate method of seeing this).
Explanation:
For those more visually or geometrically oriented; consider the following diagram, noting that if the sum of two unit vectors is a unit vector then the 3 unit vectors can be combined into an equilateral triangle:
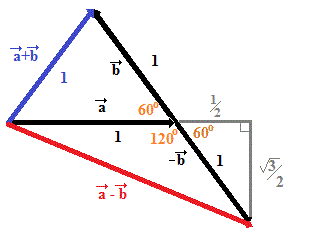
By extending the initial unit vector and dropping a perpendicular to that extension from the terminal point of the vector
we have a right triangle with sides:
So

