Question #50f95
1 Answer
Unit conversions with scientific notation are all about base 10 exponents.
Explanation:
I'll show you how to do a couple of conversions using scientific notation and then redirect you to some videos.
When you're doing unit conversion with scientific notation, you have to keep track of the base 10 exponents. If you're converting between two SI units, the base 10 exponents will be the only ones that change.
Until you get used to the multiplication factors that get you from one unit to another, use a metric conversion chart.
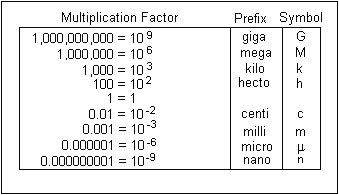
So, in your case, you have
This means that you need 1000 g to make a kg, or, in other words, that 1 kg contains
Notice that you only had to work with the base 10 exponents.
Now let's say that you want to convert this value to micrograms. The multiplication factor is equal to
You would write
Now let's say that you want to convert to gigagrams. The multiplication factor is equal to
Now, let's say that you want to convert to ounces. The conversion factor between these two units has 1 ounce equal to 28.3495231 grams. This time, the base 10 exponent is not the only one that changes. You would write
Two things to notice here
- You divide the regular numbers first, and leave the base 10 number unchanged;
- Then you use the base 10 number to express the result in scientific notation.
You can check out the videos available on Socratic:
http://socratic.org/chemistry/measurement-in-chemistry/unit-conversions/videos
Other videos:

