Question #4d59d
1 Answer
The ratio between distance and displacement is
Explanation:
You know that your object covered a distance of 5 m along a semicercular path. The displacement of the object is the shortest distance between its starting point and its finish point.
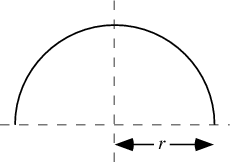
The distance it covered is equal to half of the length of a circle.
Let's say the object started at the far left of the semicircle and ended on the far right of the semicircle. The shortest distance between these points is actually the diameter of the circle.
You know that the distance is equal to 5 m, so you can write
The ratio between distance and displacement will thus be
The ratio is unitless because you're dividing meters by meters.

