Question #e3582
2 Answers
I found:
Time in air
Impact velocity:
Range:
BUT please check my math!!! (I did in a hurry!!!)
Explanation:
Try this:
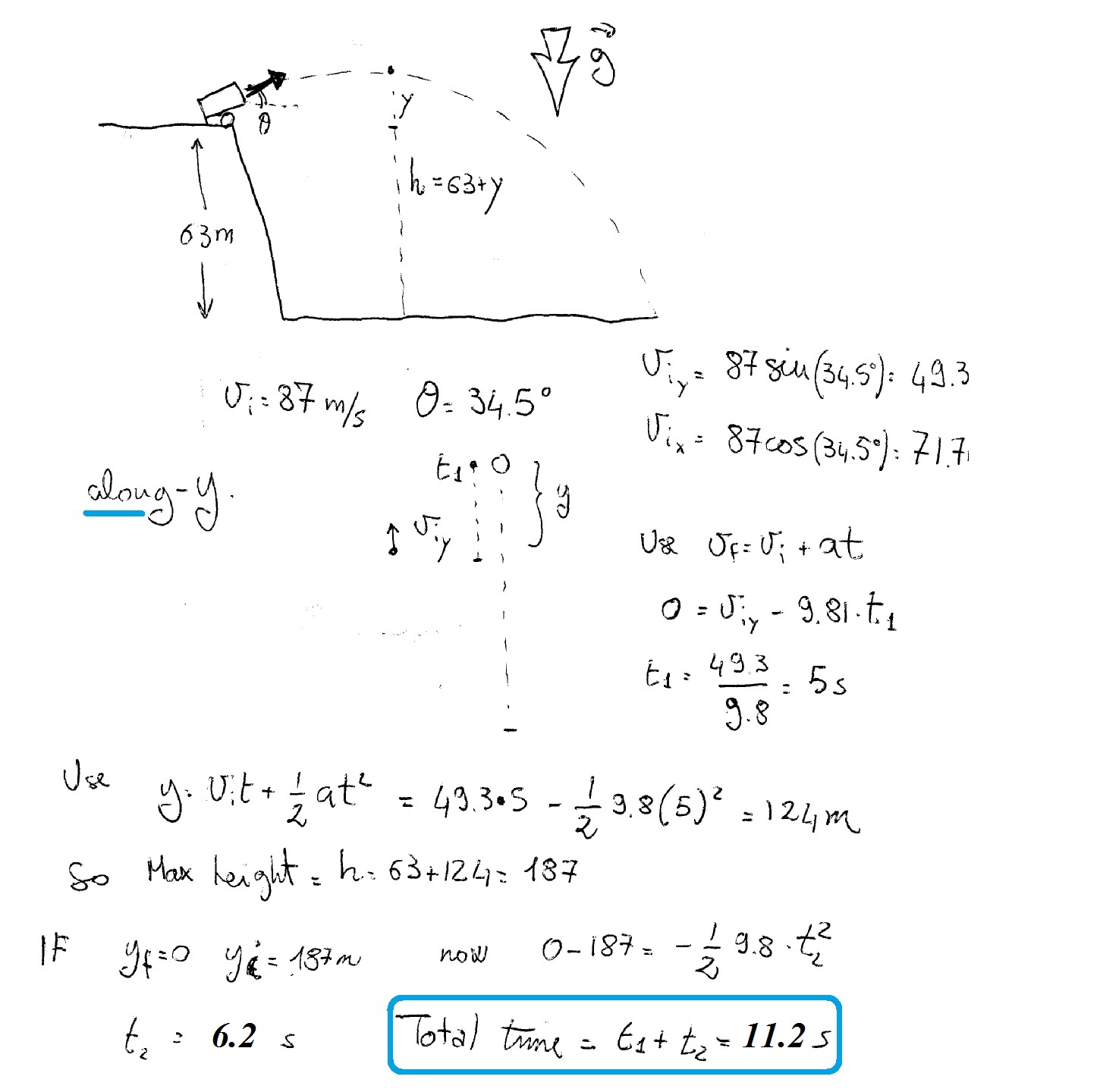

The time of flight is 11.2 s.
The velocity upon impact is 93.8 m/s.
The horizontal distance covered is 803 m.
Explanation:
So, your cannon is fired from a height of 63 m. Since the cannonball is not fired at a
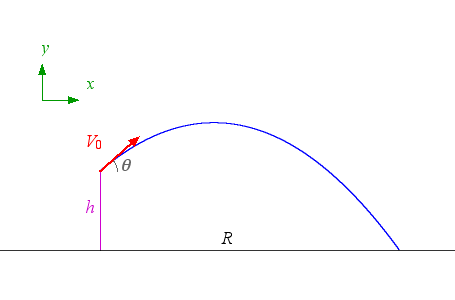
The motion of the cannonball can be described using a horizontal component and a vertical component.
Vertically, the cannonball will be under the influence of the gravitational acceleration,
You can write the equation that descibes the total vertical displacement like this
Plug in your values to get
This quadratic equation will produce two values for
Pick the positive value to get the total flight time of the cannonball
Horizontally, the movement of the cannonball is not acted upon by any forces. This means that you can write
The horizontal distance from the cliff will thus be equal to
To get the velocity of the cannonball upon impact, you need to first determine the vertical and horizontal component of this velocity.
Since horizontally the motion is constant, the velocity will be equal to
The vertical component, however, will change. You can get it by considering the fact that, at maximum height, the vertical component of the velocity will be zero.
You need to determine how much time does it take for the cannonball to go from the peak of its trajectory to the ground. Use the first part of the movement to help you with that
This means that the cannonball fell for
Therefore, the vertical component of the velocity will be
Use Pythagoras' theorem to determine the final velocity


