Question #b76e5
1 Answer
Here's how you would determine how many moles of a substance you have.
Explanation:
Depending on what exactly you're dealing with, you can have
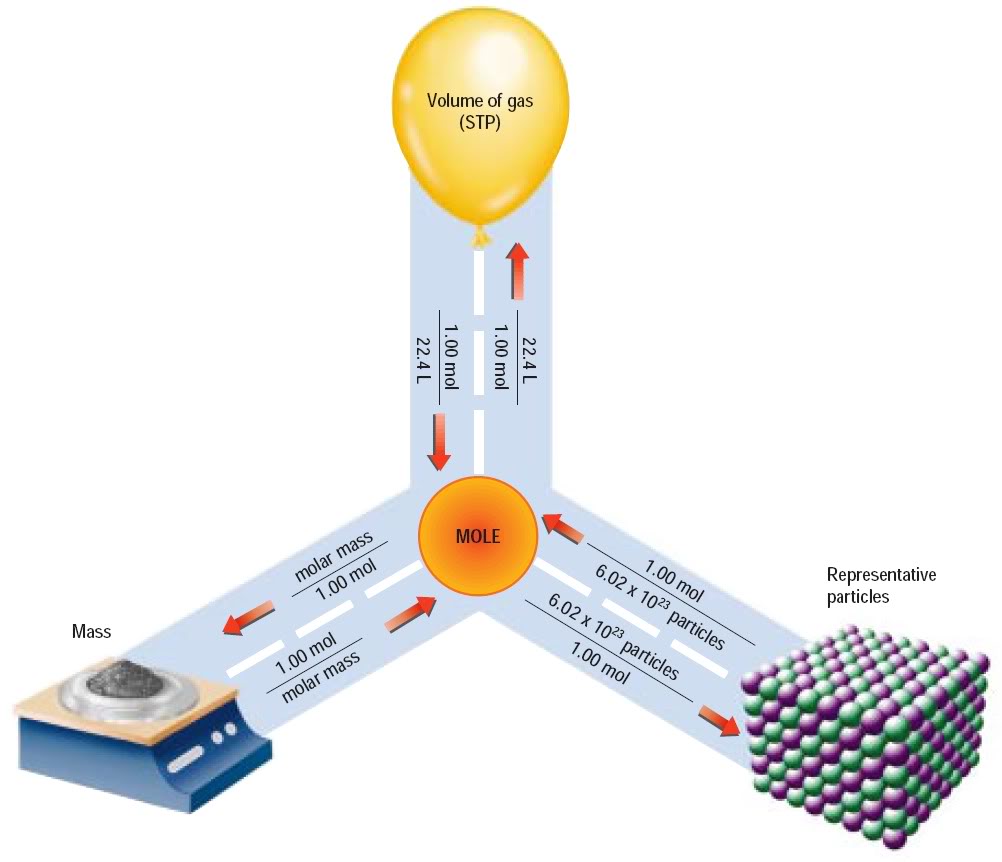
- Determine the number of moles from mass
The molar mass is the most important tool you have at your disposal when tyring to determine number of moles present in a sample.
The molar mass of a substance tells you what the mass of 1 mole of that substance is. This means that you can use it to convert between mass and moles and vice versa.
So, if you know the mass of a substance, you acn use its molar mass to determine how many moles would be present in the sample.
In other words, if you have
Likewise, if you know the number of moles you have, you can use the molar mass to get the mass of the sample.
I you have
- Determine the number of moles from the number of particles
One mole of any substance contains exctly
- Determine the number of moles of an ideal gas at STP
If you're dealing with gases, you can use the molar volume of a gas at STP to get the number of moles present in a volume of gas.
At STP, 1 mole of any ideal gas occupies exactly 22.4 L. This means that, if you have 22.4 L of a gas, you'll have one mole present.
If you have a gas that occupies a volume of