Question #4aee4
1 Answer
Here's one way in which you can convert these units.
Explanation:
In order to convert from one unit to another, you need to use conversion factors.
Conversion factors express the relationships that exist between various units. For example, the conversion factor that takes you from miles to kilometers looks like
This means that, for every 1 mile, you get 1.609344 kilometers. The other conversion factors you'll use are actually metric multiples.
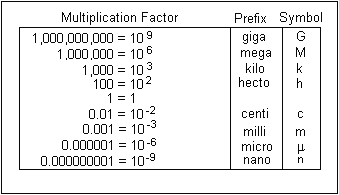
So, start with the first one. You need to go from miles per hour to kilometers per hour, then to meters per hour, and finally to meters per second.
Now for the second one. You need to get from kilograms per cubic meter to grams per cubic centimeters, so you're going to use two conversion factors.

