Let us first review some core concepts before answering this question. Of course we need to know the energy stored in the capacitor, or rather the energy stored in the electric field created by the charge stored in the capacitor. For this we have the formula #E=1/2Q^2/C# with #C# the capacity of the capacitor and #Q# the charge stored on one of the capacitors plates. [1]
So in order to know how the energy decreases, we need to know how the charge decreases. For this there are a few things we should keep in mind. The first thing is, is that the charge can only decrease if it can go anywhere. The simplest scenario is that the two plates are connected via a wire, so that the plates can exchange charge so they will become neutral. The second thing is that if we'd assume the wire to have no resistance, the charge would be able to move instantaneously, so the energy would fall to zero at that rate as well. Since this is a boring situation, and besides, not really realistic, we assume the wire to have some resistance #R#, which we can model by connecting the capacitors plates via a resistor with resistance #R# using resistance-less wires.
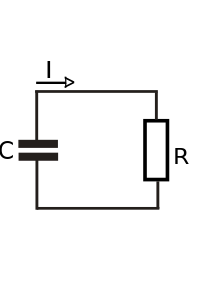
What we now have is a so called RC-circuit, seen below. In order to find out how the stored charge changes, we need to write down some differential equation. I'm not sure how proficient the reader is in math, so please let me know if the following section is unclear to you, and I'll try to explain it in more detail.
First of all we note that when we walk along the wire, we experience two jumps electric potential (voltage), namely at the capacitor and at the resistor. These jumps are given by #DeltaV_C=Q/C# and #DeltaV_R=IR# respectively [1]. We note that initially there is no current, so the potential difference over the resistor is 0, however, as we will see, there will be a current when the charges start to move. Now we note that when we walk around the circuit starting from one point, we will end up in that same point again, because we're in a circuit. At this single point the potential is the same both times, because it is the same point. (When I say we walk along the circuit, I don't mean this literally, rather we inspect the voltage jumps on the circuit at one point in time, so no time passes when walking along the circuit, therefore the argument holds, even if the voltage changes in time.)
This means that the total potential jump is zero. So #0=DeltaV_R+DeltaV_C=IR+Q/C#. Now we think about what #I#, the current is. Current is moving charge, it takes positive charge away from one capacitor plate and delivers is to the other. (Actually most of the time it's the other way around, but it doesn't matter for the mathematics of this problem.) This means that the current equals the change in charge on the plates, in other words #I=(dQ)/dt#. Substituting this in the equation above gives us #(dQ)/dtR+Q/C=0#, which means #(dQ)/dt=-Q/(CR)#. This is a so called linear first order differential equation. It dictates the change in the charge by the value of the charge at that time in a linear way, meaning that if the charge were twice as big, the change in charge would be twice as big as well. We can solve this equation by clever use of calculus.
#(dQ)/dt=-Q/(CR)#, we assume #Qne0#, which it isn't initially, and as it will turn out, it will never be. Using this we can say #1/Q(dQ)/dt=-1/(CR)#. To know #Q# at some point in time #t# (in other words #Q(t)#, we integrate the equation as follows: #int_0^t1/(Q(t'))(dQ(t'))/(dt')dt'=int_0^t-1/(CR)dt'=-t/(CR)# since #C# and #R# are constants. #int_0^t1/(Q(t'))(dQ(t'))/(dt')dt'=int_(Q(0))^(Q(t))(dQ)/Q=ln((Q(t))/(Q(0)))# via change of variables. This means #ln((Q(t))/(Q(0)))=-t/(CR)#, so #Q(t)=Q(0)exp(-t/(CR))#.
Lastly we need to substitute this back in the equation for the energy:
#E(t)=1/2(Q(t)^2)/C=1/2(Q(0)^2)/Cexp(-2t/(CR))=E(0)exp(-2t/(CR))#.
So the energy falls exponentially through time. Indeed we see that if #R# were to go to zero, #E(t)# would go to 0 instantly.
[1] Griffiths, David J. Introduction to Electrodynamics. Fourth edition. Pearson Education Limited, 2014


