Question #02b85
1 Answer
Explanation:
One thing you can do is start by multiplying both sides of the equation
Next, rearrange this to get
Now square both sides to get
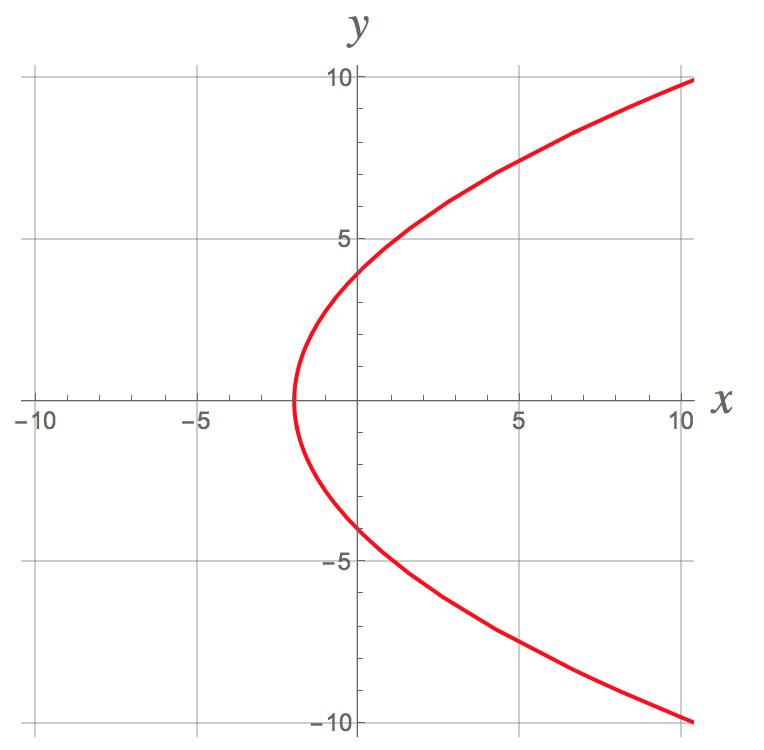
The reason this was a good idea is that you can now substitute rectangular coordinates
#x^2+y^2=16+8x+x^2#
#y^2=16+8x# .
Solving this equation for
#x=(1/8)(y^2-16)=1/8 y^2-2# .
The graph of