Question #b9611
1 Answer
That depends on how many grams of 20-carat gold you have.
Explanation:
Now, since you didn't provide an actual mass of 20-carat gold, I'll use
Now, the first thing that you need to do is figure out how much gold you have in
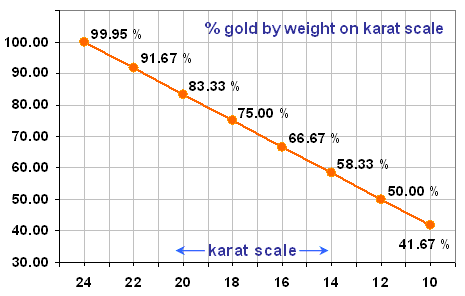
As you can see, 20-carat gold contains 83.33% gold by weight. This means that a 100-g sample of 20-carat gold will contain 83.33 g of pure gold.
In your case,
#xcolor(red)(cancel(color(black)("g 20-carat"))) * "83.33 g gold"/(100color(red)(cancel(color(black)("g 20-carat")))) = (0.833 * x) " grams of gold"#
Use gold's molar mass, which tells you what the mass of 1 mole of gold is, to determine how many moles of gold you'd get in that mass
#(0.833 * x)color(red)(cancel(color(black)("g gold"))) * "1 mole Au"/(196.97color(red)(cancel(color(black)("g gold")))) = (0.00423 * x)" moles Au"#
To get how many atoms of gold you'd get in that many moles, use the fact that 1 mole of any element contains exactly
In your case, that many moles would contain
#(0.00423 * x)color(red)(cancel(color(black)("moles Au"))) * (6.022 * 10^(23)"atoms of Au")/(1color(red)(cancel(color(black)("mole Au")))) = (2.55 * x) * 10^(21)"atoms of Au"#
To get the actual answer, simply replace
ADDENDUM
For 20 g of 20-carat gold, you would get
#2.55 * 20 * 10^(21) = 5.1 * 10^(22)"atoms of Au"#

