Molecular orbital theory for polyatomic molecules?
1 Answer
There kind of is, but it builds off of molecular orbital theory and is very difficult to articulate in an accessible way.
The core premises of this method are:
- In a molecule with more than two atoms, any orbitals with directional aspects (i.e. not spheres) pointing towards the central atom are considered to be along the
#\mathbf(y)# axis (rather than the#z# axis). - Each atom surrounding a central atom is considered to have its own set of axes. So, each atom has different
#x# and#z# axes. - The orbitals of the surrounding atoms are considered to "transform" as "group orbitals", meaning that they bond to the atoms of the central atom as a group.
- As usual, only compatible orbitals can overlap with each other (just like in MO theory).
As a brief overview of the idea of individual axes, consider this image of a tetrahedral set of axes:
This gets complicated very quickly, so I'll simply work with
We will be using a method called Symmetry-Adapted Linear Combinations (SALCs).
What that means is that we'll determine how to categorize certain orbitals to determine which ones are allowed to overlap. Then, we'll build the MO diagram from scratch.
The overall steps we'll be following are:
- Finding the point group.
- Finding the reducible representation based on how the hydrogen atoms behave.
- Reducing the reducible representation to its irreducible representations.
- Assigning those to the group of hydrogens.
- Determining which orbitals are compatible.
- Making the MO diagram.
SYMMETRY CONSIDERATIONS
Ammonia belongs to what is called the
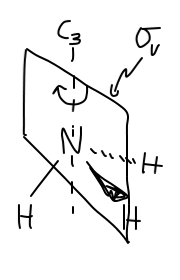
A
A
DETERMINING THE REDUCIBLE REPRESENTATION
The irreducible representations, or IRREPs, are what we will use to categorize the ways the hydrogens "behave" around the nitrogen.
Given that
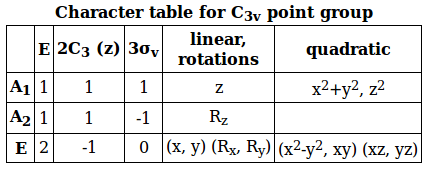
To determine the irreducible representations, we first need the reducible representations,
- For each symmetry element (
#E# , the identity,#C_3(z)# , the principal rotation, and#sigma_v# , the vertical mirror plane), operate on the hydrogen atoms as a group and see where each one ends up. - The hydrogens that stay where they are and do NOT move contribute
#1# to#Gamma# .
The hydrogens that DO move contribute#0# to#Gamma# .
The hydrogens that change orbital sign contribute#-1# to#Gamma# .
Now, let's align the molecule in a more convenient way. Let the
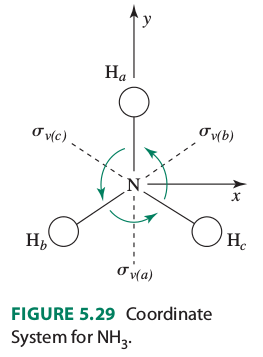
We see that there are three
#color(green)(H_a -> H_a)# #color(green)(H_b -> H_b)# #color(green)(H_c -> H_c)#
Thus, we get
#H_a -> H_b# #H_b -> H_c# #H_c -> H_a#
Each hydrogen moved, and none of them stayed where they are, so this operation contributes
#color(green)(H_a -> H_a)# #H_b harr H_c#
Since ammonia is symmetrical and each hydrogen is identical, performing
The reducible representation then, using the
#color(blue)(" "" "" "E" "C_3(z)" "sigma_v)#
#color(blue)(Gamma_(1s) = " 3"" "0" "" "" "1)#
Phew, now let's reduce this!
THE IRREDUCIBLE REPRESENTATIONS
Basically, the rows in the character table above have to add up to give

So, the group orbitals of hydrogen "transform under
This is depicted as follows:
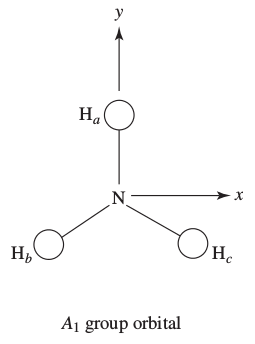
In this one, the hydrogen
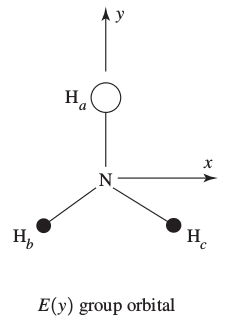
In this one, there is one hydrogen
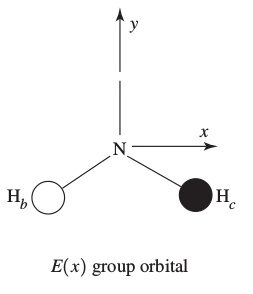
This one is similar to
FINALLY DRAWING THE MO DIAGRAM!
Okay, finally, we have enough information to draw an approximate MO diagram.
To save time (and brain), I'm just going to have to tell you the symmetries of nitrogen's orbitals. The
The orbitals will combine like so:
#"3H"# #A_1# with#"N"# #A_1# (bonding, antibonding)#"3H"# #E(x)# with#"N"# #E# (bonding, antibonding)#"3H"# #E(y)# with#"N"# #E# (bonding, antibonding))#"Nothing"# with#"N"# #A_1# (nonbonding)
Using the orbital potential energies (Appendix B.9) of each atom, we eventually get:
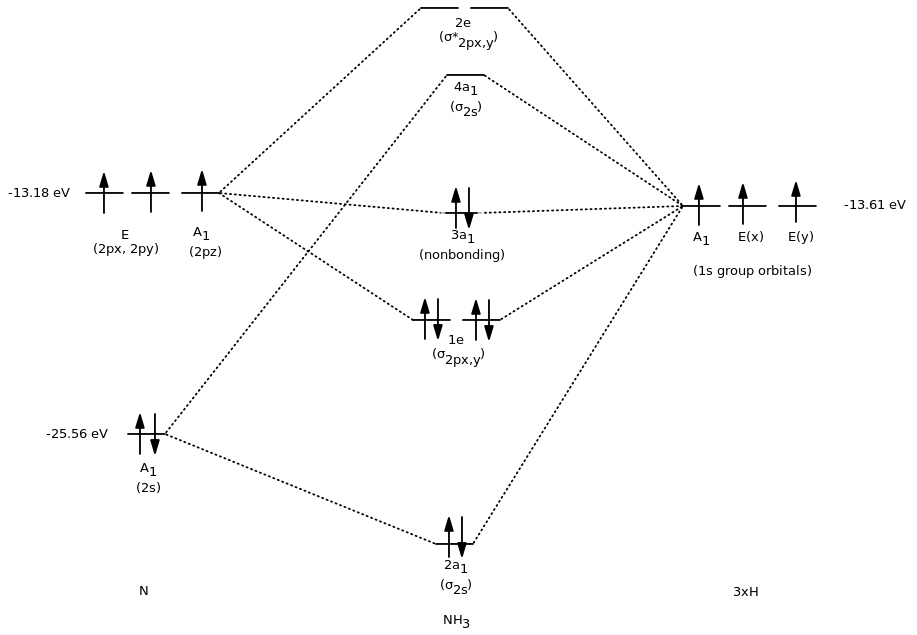
Note that we came in with seven orbitals (
Also note that only the orbitals of the same symmetry (
The first three bonding MOs of
And here is a reference (Inorganic Chemistry, Miessler et al., pg. 156) to show the actual MO diagram.

