Question #5d5a2
1 Answer
Here's how you can solve this problem.
Explanation:
Water of a river, that is 1000m wide and has parallel banks, flows towards north in a constant velocity of
- What is the boat's velocity relative to earth?
- When the boat reaches the next bank, what is the distant it has flowed down the river?
- What is the time taken for the man to cross the river?
If the man wants to get to the point perpendicular to the point he starts rowing, with all the other vectors same as above
- What is the direction he has to row the boat?
- Then, what is the boat's velocity relative to the earth?
- What is the time taken for the man to reach the other bank of the river?
So, you know that the river is 1000 m wide. The boat moves with a constant speed of
If you take the north direction to be the
#v^2 = v_x^2 + v_y^2#
The magnitude of the velocity of the boat relative to the bank of the river will be equal to
#v = sqrt(v_x^2 + v_y^2)#
#v = sqrt(3^2 + 2^2)"ms"^(-1) = color(green)("3.61 ms"^(-1))#
Now, the boat will move at an angle of
#tan(theta) = v_y/v_x implies theta = arctan(v_y/v_x)#
#theta = arctan((2color(red)(cancel(color(black)("ms"^(-1)))))/(3color(red)(cancel(color(black)("ms"^(-1)))))) = color(green)(33.7""^@)#
The velocity of the boat will thus be
You can find the distance the boat travelled down river by taking into account the fact that the width of the river is covered with a speed of
Likewise, the distance travelled downstream will be covered with a speed of
This means that you can find the time needed to cross the river by using
#underbrace(d_"x")_(color(blue)("width of river")) = v_x * t#
#t = d_x/v_x = (1000color(red)(cancel(color(black)("m"))))/(3color(red)(cancel(color(black)("m")))"s"^(-1)) = "333.3 s"#
Since the time needed to cross the river is the same for both directions, you can say that
#underbrace(d_y)_(color(blue)("distance downstream")) = v_y * t#
#d_y = 2"m"color(red)(cancel(color(black)("s"^(-1)))) * 333.3color(red)(cancel(color(black)("s"))) = color(green)("667 m")#
Now, for the second part of the problem, you need to find the direction the boat must take in order to reach the other bank in a point directly across its starting point.
All you really need to do here is flip the triangle vertically formed with the width of the river and the distance travelled downstream.
Since all vectors remain unchanged, it follows that the boat must start rowing at an angle of
#theta_2 = -33.7""^@#
The minus sign symbolizes the fact that this angle is measured below the
The magnitude of the velocity of the boat will be the same
#v = sqrt(v_x^2 + v_y^2)#
#v = sqrt(3^2 + 2^2)"ms"^(-1) = "3.61 ms"^(-1)#
The velocity of the boat will be
Of course, the boat will reach the other bank in the same period of time,
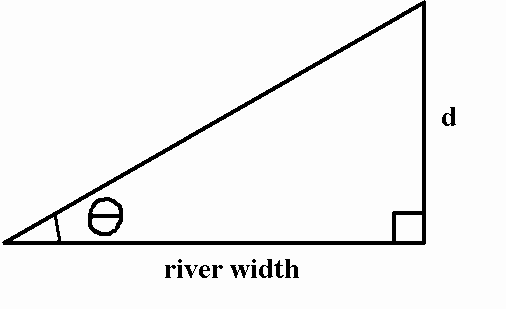
Here's what I mean by flipping the triangle. The boat starts crossing the river, and
If all vectors are kept the same, all you have to do is
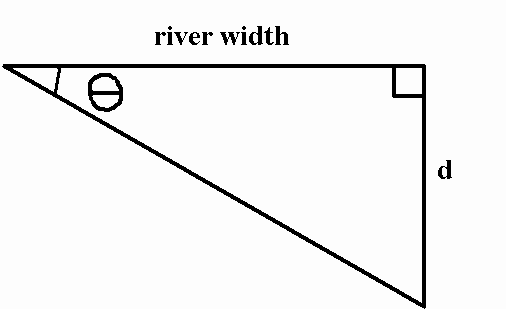
This time, the boat will start moving at an angle

