Here is sketch of the problem:
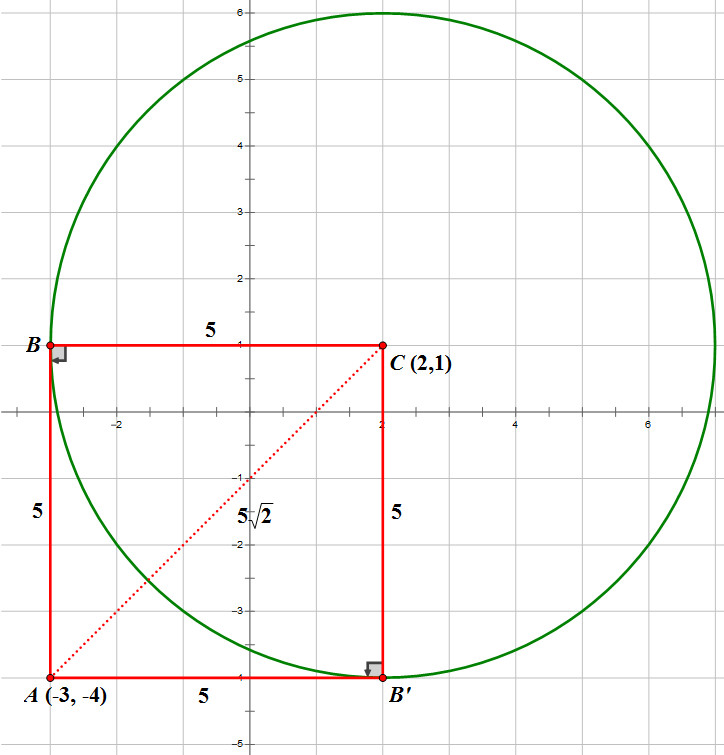
There are exactly two lines that will pass through the point (-3, -4) and that will also be 5 units away from the point (2,1).
Drawing a circle with radius = 5 helps to visualize the problem.
Notice that both lines #bar(AB) and bar(AB'# are tangent lines to the circle. Also note, #/_ ABC and /_AB'C# are both right angles formed by the tangent lines and the radii of the circle.
Both lines #bar(AB) and bar(AB'# show a length of 5 units. Let's prove that now:
#Delta#ABC and #Delta#AB'C are both right triangles that are congruent by the theorem HL (hypotenuse-leg). We can calculate the length of the hypotenuse by using the distance formula between two points (I'll leave that for you to prove). The length of #bar(AC)# is #5sqrt2#. Finally, use the Pythagorean Theorem to find the length of #bar(AB) and bar(AB'# which both are equal to 5 units. This implies that the coordinate of point B is (-3, 1) and point B' is (2, -4) which means #bar(AB)# is vertical line and #bar(AB')# is a horizontal line .
Now we have all the information we need to determine the equations of the two lines #bar(AB) and bar(AB'#:
#bar(AB)# is a vertical line #x =-3#
#bar(AB'# is a horizontal line #y =-4#
Hope that helped!


