Question #75f44
1 Answer
Momentum, according to Newton's idea, is Q=m*v. It means that mass is important, but not just mass, also speed. Initially mass is important, but in "high" speed, speed is important.
Explanation:
If both the truck and the Ferrari is in rest, the momentum of the truck and Ferrari is the same (Q=m*v, Q=0) (1)(2), but in case they are in movement, the Ferrari's will be higher since it can reach higher speeds.
Another example is a watermelon, it can kill a person if falling from a tall building, but it is "useless" for that purpose in low speeds. Another example are bullets, it can "throw away" a human body in the impact.

The answer is simple, it depends on the speed of the truck and Ferrari , mass is important, but not just mass.
Example:
Consider a reference value:
Then, for the truck:
For the Ferrari,
Of course it is just mathematical trick, try it with real values!
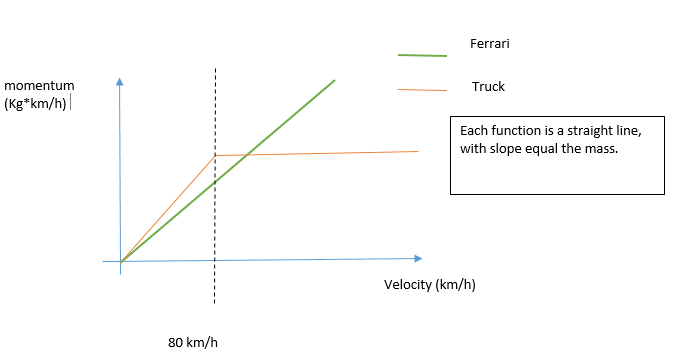 Attention on this graph, it is representative, when the red line becomes constant, it should "stop", bearing in mind our truck cannot exceed 80 km/h.
Attention on this graph, it is representative, when the red line becomes constant, it should "stop", bearing in mind our truck cannot exceed 80 km/h.

