Question

When are bonding or antibonding orbitals needed? What info can be gotten from knowing their occupations?

Answer 1

All molecules have both bonding and antibonding molecular orbitals, but only some have electrons in those antibonding orbitals. That usually tells you how many bonds it has, and sometimes something about the stability of the molecule.

I'll try to make it "simple", but I will go for "accessible".

If you meant why there are both bonding and antibonding, it's because orbitals, being waves, can overlap out-of-phase or in-phase. Depending on the type of atomic orbital, you get either the bonding or antibonding molecular orbital.

---

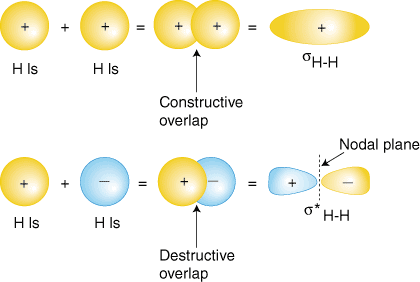
If you meant why some molecules use their antibonding orbitals and some others don't, read on.

The general idea is that if a molecule has a certain number of electrons contributed from each atom, if certain orbitals are filled, it needs to add those electrons to higher-energy orbitals, according to the Pauli Exclusion Principle and the Aufbau principle.

If you are unfamiliar with those principles, they respectively result in the idea that you can have two electrons per orbital (each electron of opposite spin) and you must add electrons into orbitals from the lowest to the highest energy because energetic ease is favorable.

For example, here is a ground-state molecular orbital diagram for `"Be"_2`, a homonuclear diatomic (two-atom molecule with identical atoms) with the atomic number `2`.

This diagram is saying that the `sigma_(2s)` bonding orbital is lower in energy than the `sigma_(2s)^"*"` antibonding orbital, and likewise for the `sigma_(1s)` and `sigma_(1s)^"*"`. It also says that each `"Be"` contributes four electrons (two from the `1s` and two from the `2s`).

Antibonding orbitals just happen to be higher in energy than the corresponding bonding orbital, so when the bonding orbital(s) is/are filled, the corresponding antibonding orbital has to start filling up with electrons.

From this diagram, you could also say that the bond order, or the "average number of bonds" between the two atoms, is `\mathbf(0)` because the number of bonding electrons is the same as the number of antibonding electrons.

That really says that `"Be"_2` is unstable in nature and is difficult to observe in real life as a homonuclear diatomic molecule.