Question

Four marbles of radius `3/8` inch are placed in a cylindrical container. The first three marbles fit snuggly with the fourth marble on top. The cylinder is then filled with water up to the top of the fourth marble. What is the volume of water?

Answer 1

`9/64pi` cubic inches

Explanation:

`4` marbles each with a diameter of `3/4` in. when stacked one on top of another will have a height of
`color(white)("XXX")h=4xx3/4 = 3` inches

Each marble will have a volume of
`color(white)("XXX")V_("marble") = 4/3pir^3`
`color(white)("XXXXXXX") =4/3pi(3/8)^3`
`color(white)("XXXXXXX")=9/128pi`
and the 4 marbles will have at total volume of
`color(white)("XXX")V_("4marbles")= 4xx9/128pi =9/32pi`

The cylinder containing them (up to the height of the fourth marble has a volume of:
`color(white)("XXX")V_("cylinder")= pir^2h`
`color(white)("XXXXXXX")=pi(3/8)^2*3`
`color(white)("XXXXXXX")=27/64pi`

The Volume of the water (i.e. the volume of the cylinder not occupied by the marbles) is
`color(white)("XXXXXXX")V_("water") = V_("cylinder")-V_("4marbles")`
`color(white)("XXXXXXX")=27/64pi-9/32pi`

`color(white)("XXXXXXX")=(27-18)/64pi`
`color(white)("XXXXXXX")=9/64pi`

`color(white)("XXXXXXX")~~0.44` (cubic inches)

Answer 2

`pi (36sqrt(3)+21sqrt(6)+36sqrt(2)-9)/256 "inches"^3 ~~ 1.910785 "inches"^3`

Explanation:

Denote the radius of a marble by `r = 3/8"inch"`

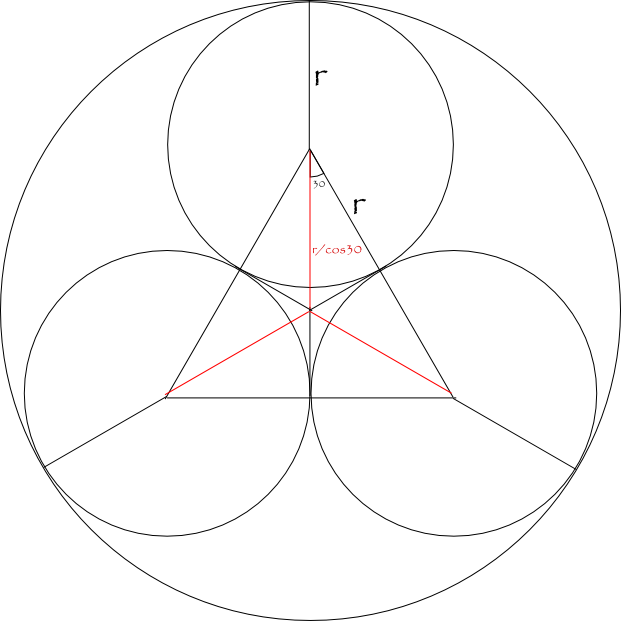
Then the radius of the cylinder is:

`r + r / cos(30^@) = r + r / (sqrt(3)/2) = r + ((2r)/sqrt(3)) = r+(2sqrt(3)r)/3 = r((3+2sqrt(3))/3) = (3+2sqrt(3))/8 "inches"`

Next, the total height of the stack of marbles will be `2r` plus the height of a tetrahedron with edges of length `2r`.

From some slightly messy calculations, the height of a tetrahedron with edges of length `2r` is `(2sqrt(6))/3r`...

Viewed from one side, the tetrahedron looks like a triangle with base of length `sqrt(3)r` and other two sides of length `sqrt(3)r` and `2r`. We want to calculate its height `h`. Drop a perpendicular from the top of the triangle to the bottom to give two right angled triangles.

Then:

`sqrt(3)r = sqrt((sqrt(3)r)^2 - h^2) + sqrt((2r)^2 - h^2)`

`= sqrt(3r^2-h^2) + sqrt(4r^2-h^2)`

Square both sides to get:

`3r^2 = 3r^2-h^2+4r^2-h^2 + 2sqrt((3r^2-h^2)(4r^2-h^2))`

Hence:

`sqrt((3r^2-h^2)(4r^2-h^2)) = h^2-2r^2`

Square both sides again to get:

`(3r^2-h^2)(4r^2-h^2) = (h^2-2r^2)^2`

That is:

`12r^4-7r^2h^2+h^4 = h^4-4h^2r^2+4r^2`

So:

`8r^4 = 3h^2r^2`

Divide both sides by `3r^2` and take square root to find:

`h = sqrt(8)/sqrt(3)r = (2sqrt(6))/3r`

So the total height of the stack of marbles is:

`2r + (2sqrt(6))/3r = (6+2sqrt(6))/3r = (6+2sqrt(6))/8 "inches" = (3+sqrt(6))/4 "inches"`

The volume of the cylinder up to this height is:

`"{area of circle}" xx "{height}"`

`=pi ((3+2sqrt(3))/8)^2 xx (3+sqrt(6))/4 "inches"^3`

`=pi ((21+12sqrt(3))/64) xx (3+sqrt(6))/4 "inches"^3`

`=pi (63+36sqrt(3)+21sqrt(6)+36sqrt(2))/256 "inches"^3`

The volume of each marble is:

`4/3 pi r^3 = 4/3 pi (3/8)^3 "inches"^3`

`= pi 9/128 "inches"^3`

So the volume of four marbles is:

`= pi 9/32 "inches"^3`

So the total volume of water will be:

`pi (63+36sqrt(3)+21sqrt(6)+36sqrt(2))/256 "inches"^3 - pi 9/32 "inches"^3`

=`pi (63+36sqrt(3)+21sqrt(6)+36sqrt(2))/256 "inches"^3 - pi 72/256 "inches"^3`

=`pi (36sqrt(3)+21sqrt(6)+36sqrt(2)-9)/256 "inches"^3`