Question #8c69f
1 Answer
Explanation:
The idea here is that the rate of effusion of a gas, that is, the number of moles of gas per unit of time, is inversely proportional to the square root of its molar mass - this is known as Graham's Law.
#"rate" prop 1/sqrt(M_M)#
In other words, the heavier each individual molecule of a gas is, the slower it will effuse. LIkewise, the lighter the molecules of a gas, the faster they will effuse.
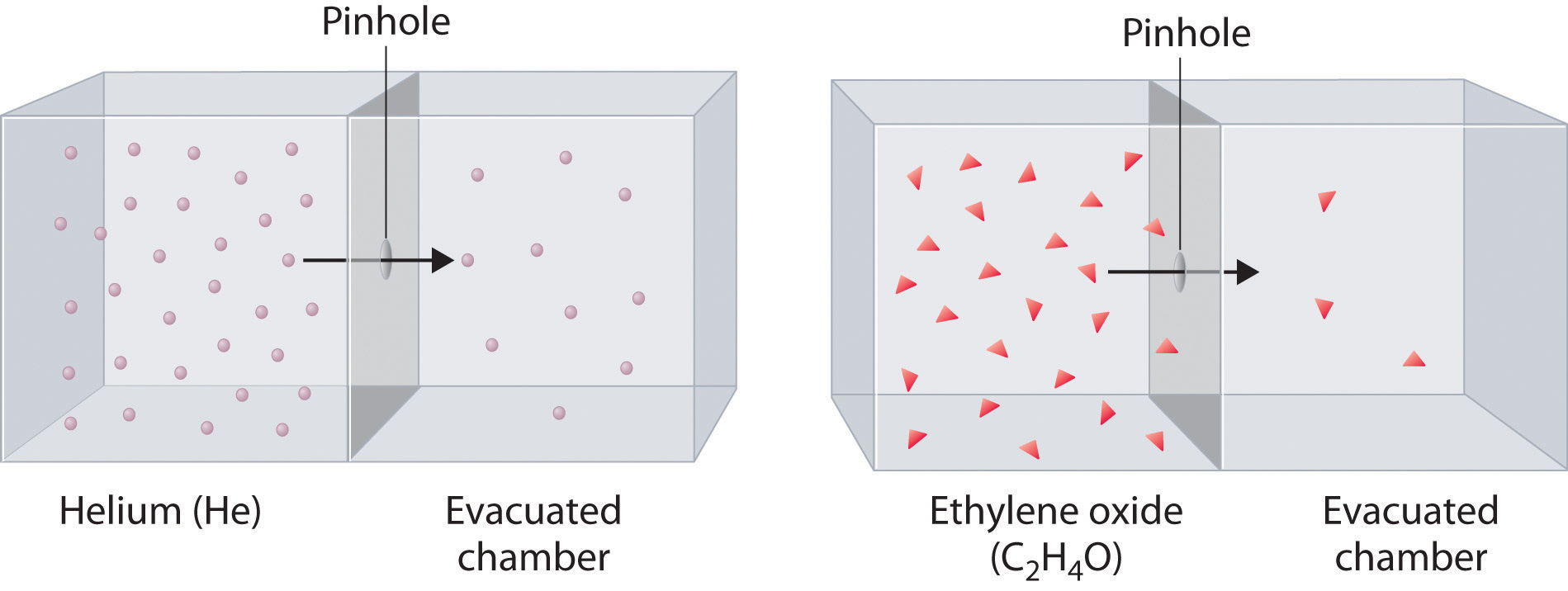
Here's how that would look for helium and ethylene oxide - notice that fewer molecules of ethylene oxide effuse when compared with the lighter helium molecules.
In your case, you know that a certain gas takes three times as long to effuse as jelium. Right from the start, you know that you're dealing with a gas that has heavier molecules than helium does.
If you take
#r_(He) = 3 xx r_(X)#
Moreover, you know that
#r_(He) prop 1/sqrt(M_"M helium")" "# and#" "r_(X) prop 1/sqrt(M_"M gas X")#
If you divide these expressions, you will find that
#r_(He)/r_(X) = 1/sqrt(M_"M helium") * sqrt(M_"M gas X")#
#(3 xx color(red)(cancel(color(black)(r_(X)))))/(color(red)(cancel(color(black)(r_(X))))) = sqrt(M_"M gas X")/sqrt(M_"M helium")#
To keep the calculations simple, you can use helium's molar mass to be
Rearrange the above equation to solve for
#sqrt(M_"M gas X") = 3 xx sqrt(M_"M helium")#
Square both sides to get rid of the square roots
#(sqrt(M_"M gas X"))^2 = 3^2 xx (sqrt(M_"M helium"))^2#
#M_"M gas X" = 9 xx "4 g/mol" = color(green)("36 g/mol")#

