Question #8685a
1 Answer
Explanation:
The area of a parallogram is given by the magnitude of the cross product of two vectors which make up two sides of the parallelogram and are not parallel to each other.
The cross product of two parallel vectors is zero. That is,
#abs(vecaxxvecb)=vec0# iff#veca"//"vecb#
- I will provide an *explanation as to how we arrive at this procedure for calculating the area at the end if you are interested.
Diagram:
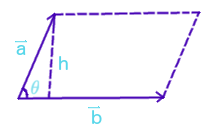
- Where
#veca=(2i-3j-k)# and#vecb=(i+4j-2k)# .
We can then find the area of the parallelogram by taking the cross product of these two vectors.
Given vectors

Where:
#color(darkblue)(uxxv=(u_2v_3-u_3v_2)veci-(u_1v_3-u_3v_1)vecj+(u_1v_2-u_2v_1)veck)#
This process may look rather complicated but in reality isn't so bad once you get the hang of it.
We have
For the
#(-3*-2)-(4*-1)=6+4=10#
For the
#-[(2*-2)-(-1*1)]=-(-4+1)=3#
For the
#(2*4)-(-3*1)=8+3=11#
Our answer is then
We then take the magnitude of this vector to find the area of the parallelogram:
#color(darkblue)(abs(vecc)=sqrt((c_x)^2+(c_y)^2+(c_z)^2))#
#=>abs(vecc)=sqrt((10)^2+(3)^2+(11)^2)#
#=>abs(vecc|=)=sqrt(100+9+121)#
#=>color(darkblue)(abs(vecc)=sqrt(230))#
And so, the area of the parallelogram is
*Explanation of equation:
-
The area of a parallelogram is given by the
#A=bh# , where#b# is the base and#h# is the height of the parallelogram. -
Using basic trigonometry, we can see from our diagram that
#sin(theta)=h/(|veca|)#
where the magnitude of the vector corresponds to the vector's length. We can rearrange to solve for h.
#h=abs(veca)sin(theta)#
- The base of our parallelogram is given by
#abs(vecb)# , the length of vector#b# . Our area equation becomes:
#A=b*asin(theta)#
- Given that
#abs(vecaxxvec)|=b*asin(theta)# , we can rewrite as:
#A=abs(vecaxxvecb)#


