Question

Question #e8be5

Answer 1

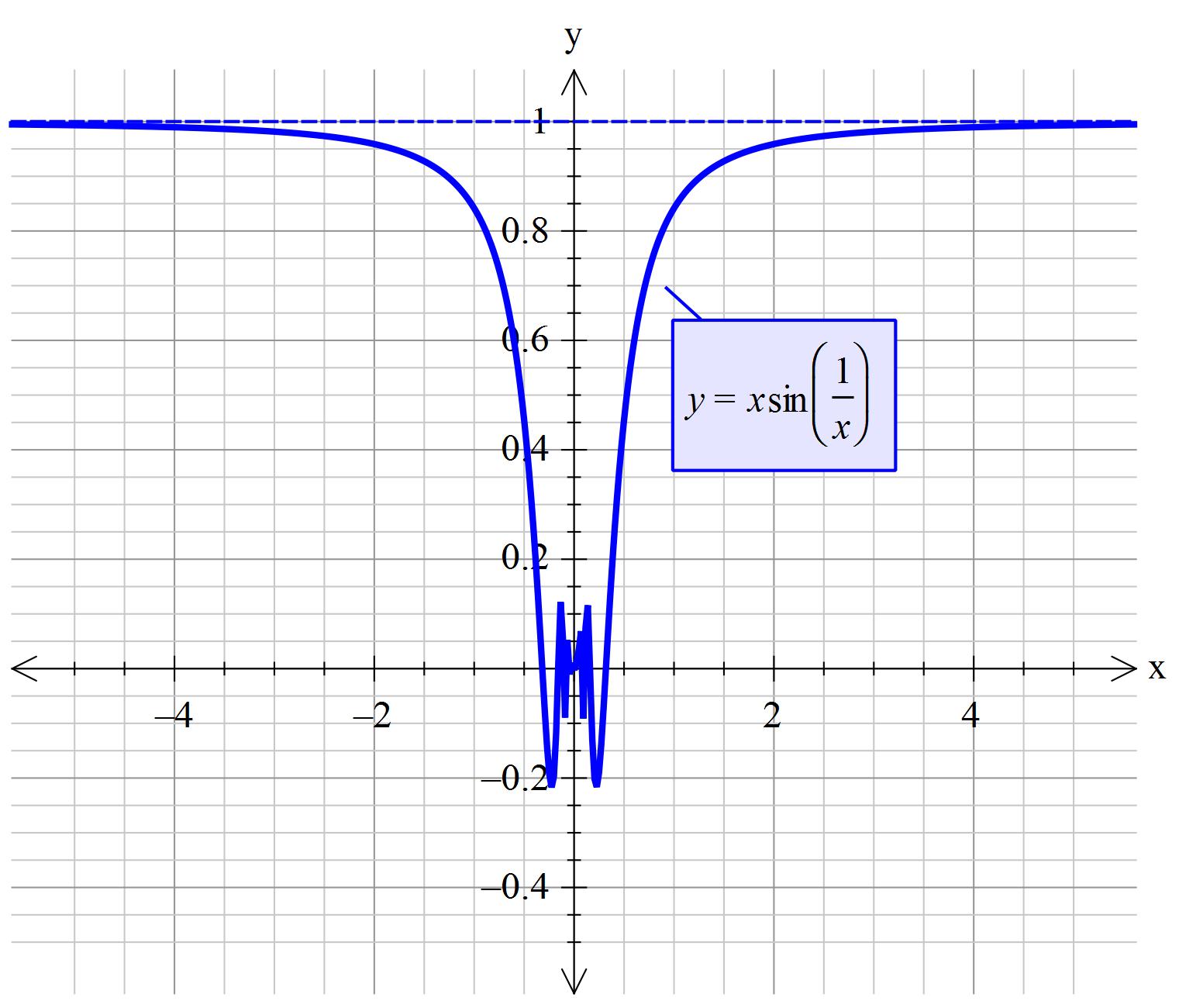
The limit is `0`

Explanation:

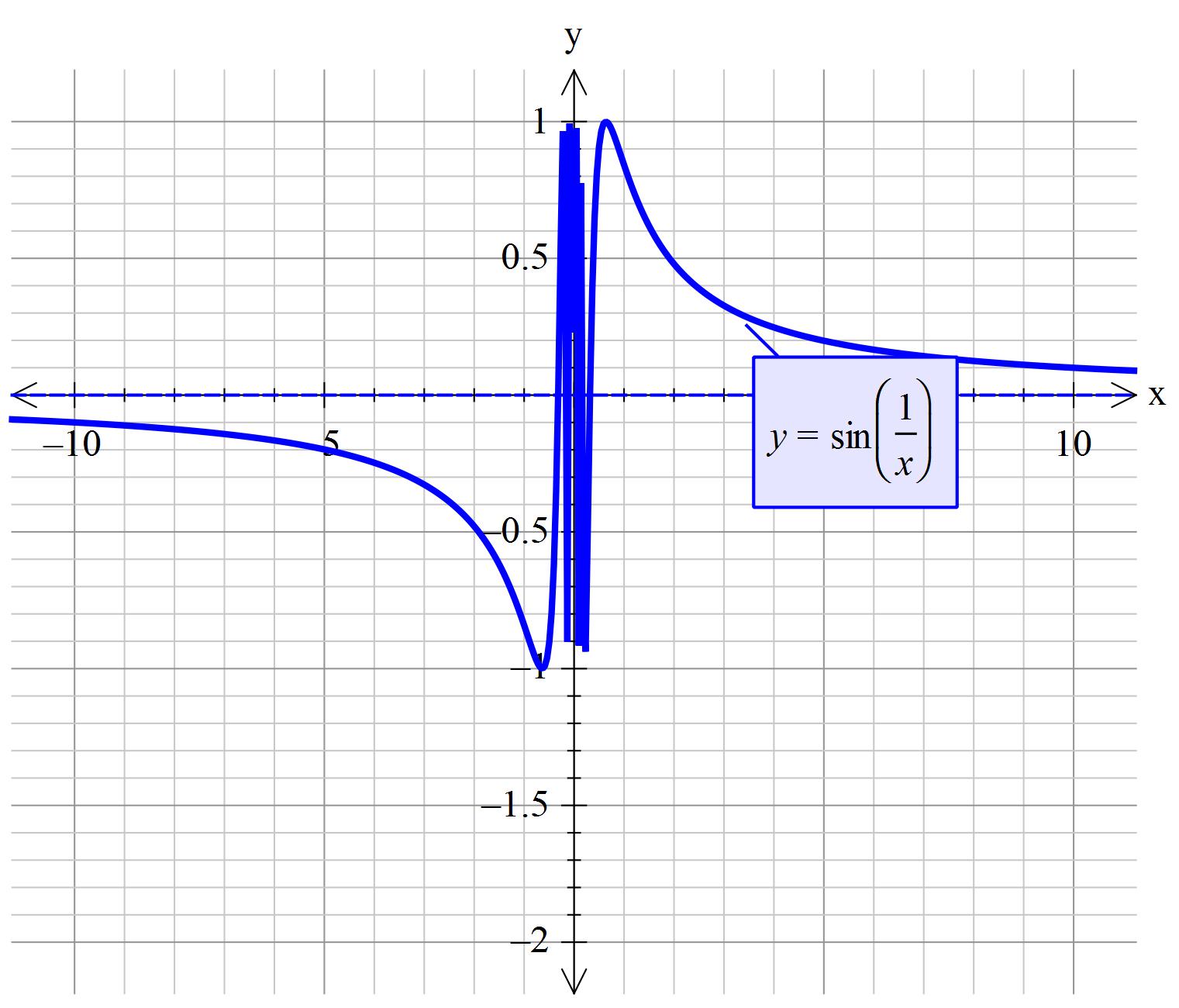
The easiest method to find this is to use the squeeze theorem. This theorem states the following in this case: suppose you find two functions `g(x)` and `h(x)` for which holds that `g(x) <= xsin(1/x) <= h(x)`.
If `lim_{x to 0} g(x) = L = lim_{x to 0} h(x)`, then it definitely holds that:
`lim_{x to 0} xsin(1/x)=L`.

The hardest part is to find two functions for which this holds.
You can do this by noticing that the sine function can only go from `-1` to `1`. This means that the function is always bigger than `-1*|x|` and always smaller than `1*|x|`:
`-|x|<= xsin(1/x)<=|x|`

Let's look at the limits of the two functions:
`lim_{x to 0} -|x| = lim_{x to 0} |x|=0`

This means that `lim_{x to 0} xsin(1/x)=0`