in spherical coordinates, using this coordinate system
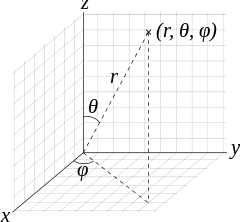
we arrange the axes so that cup in question is symmetrically placed about origin O with the centre of the flat surface at O, and we place a unit test charge #Q_t# at O to calculate the field there.
The surface element for constant radius a follows as
#dS =a^{2} \sin theta \ d \theta \ d \varphi #
Assuming a uniform charge density #sigma # on the cup, the charge of a small element is
#dq = sigma dS# where #sigma = Q/A = Q/(2 pi a^2) # ,
the force due to a given small element will follow Couloumb's Law: #F = k (Q Q_t) / r^2#
#dF = k (dq Q_t) / a^2#
the force on the unit test charge #Q_t# placed at O will be zero due to symmetry. we need only look at the force in the z-direction. so here we can say that
#dF_z = k (dq Q_t) / a^2 * cos theta#
Putting it altogether
#dF_z = k ((sigma dS) Q_t) / a^2 * cos theta #
#(dF_z)/Q_t = dE_z = k sigma / a^2 \ cos theta \ dS#
#\implies dE_z = k sigma / a^2 \ cos theta \ a^{2} \sin theta \ d \theta \ d \varphi #
#= k sigma/2 \sin 2 theta \ d \theta \ d \varphi #
and as #k = 1/(4 pi epsilon_o) #
#\implies dE_z = 1/(4 pi epsilon_o) Q/(4 pi a^2) \sin 2 theta \ d \theta \ d \varphi #
# \implies dE_z = 1/((4 pi a)^2 epsilon_o) Q \sin 2 theta \ d \theta \ d \varphi #
# \implies E_z = 1/((4 pi a)^2 epsilon_o) Q int_{varphi = 0}^{2 pi} \ int_{theta = 0}^{pi/2} \ \sin 2 theta \ d \theta \ d \varphi #
# = 2 pi 1/((4 pi a)^2 epsilon_o) Q \ int_{theta = 0}^{pi/2} \ \sin 2 theta \ d \theta #
# = 1/( 8 pi epsilon_o a^2) Q [ -1/2 \cos 2 theta ]_{theta = 0}^{pi/2} \ #
# = 1/(8 pi epsilon_o a^2) Q [ \cos 2 theta ]_{theta = pi/2}^{0} \ #
# = Q/(8 pi epsilon_o a^2) #
# = (k Q)/(2 a^2 ) #


