Question #d667a
1 Answer
Fatma's is
Ayse's is
Explanation:
You can use a velocity time graph to solve this problem.
The distance covered is represented by the area under the graph.
We can use the fact that the total distance travelled is the same so the area under the distance time graphs is the same for each runner:
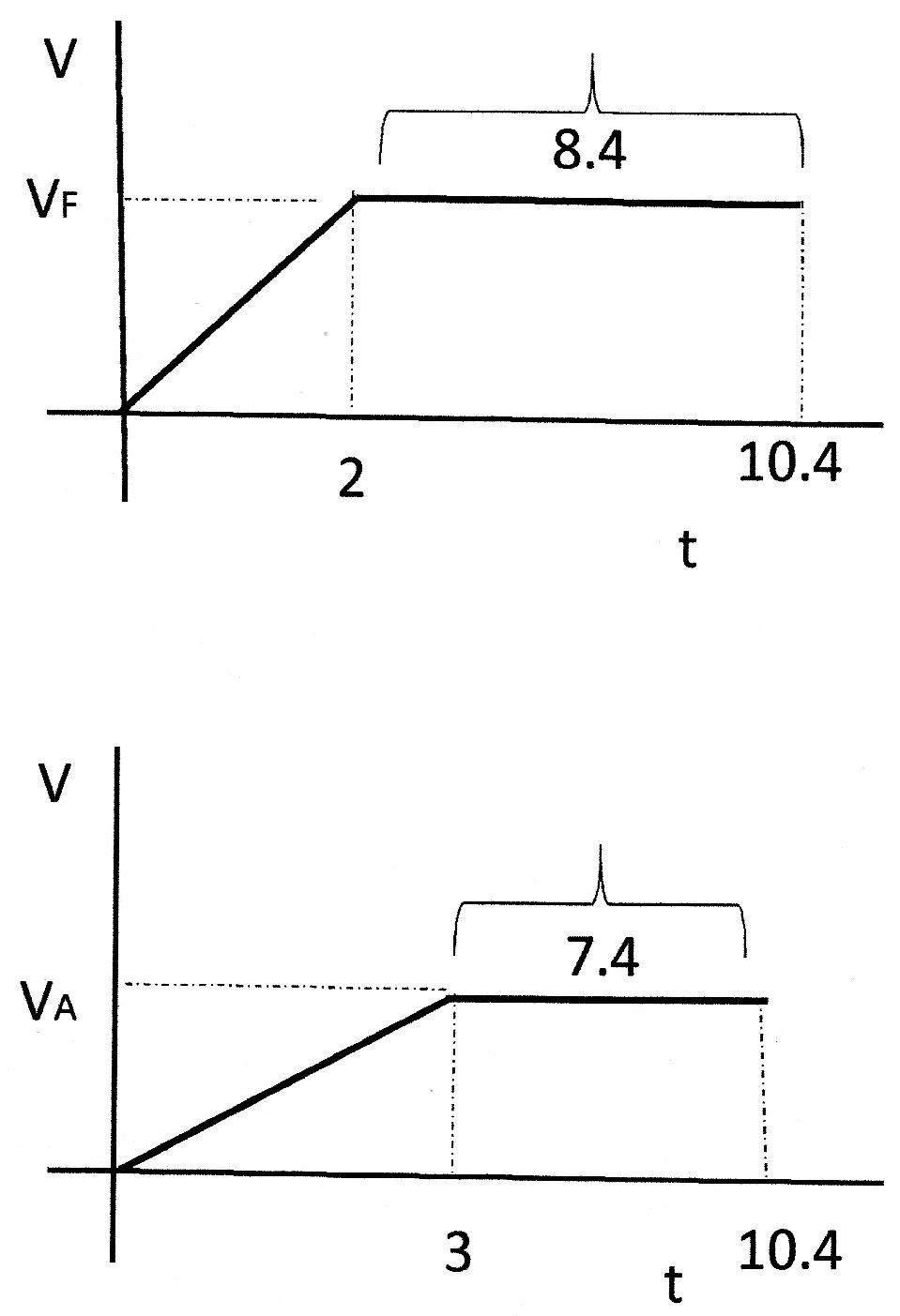
We divide the race into 2 parts. The first part is where they are accelerating.
The second part is where they are running at constant velocity.
We can find the area under each section using simple geometry.
We then add these together. The sum must equal 100m.
The area of a triangle is 1/2 x base x height.
So for Fatma:
Let
For Ayse we refer to the 2nd graph:

