Well, the atomic orbital (AO) ordering is quite normal and predictable.
BERYLLIUM AO ENERGY ORDERING
#"Be"#'s ground-state electron configuration is the one you've probably learned by now, which is #1s^2 2s^2#; that indicates that the #2s# is higher in energy (but you knew that), so all you really have is a #1s# AO, and then a #2s# AO substantially higher in energy. That's the AO diagram.
So, literally draw two horizontal lines, label them #1s# and #2s#, and draw a vertical equilibrium arrow through each orbital, pretty much.
One arrow for each electron; one is spin-up and the other is spin-down due to the Pauli Exclusion Principle (must be different quantum states; it is enough to have different #m_s#).
(I've technically still drawn it twice below.)
BERYLLIUM MO DIAGRAM OVERVIEW
What's more interesting is if you draw the molecular orbital (MO) diagram for #"Be"_2# (I did this in MarvinSketch):
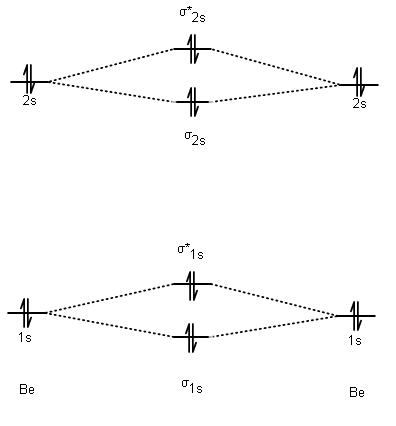
The AO diagrams are on the left or right. The MO diagram is the diagram as a whole.
If you want to draw the excited state, draw a #2p# AO a bit further above and move one #2s# electron (from the highest-occupied AO) into the #2p# AO (the lowest-unoccupied AO).
LINEAR COMBINATION OF SIGMA #\mathbf(ns)# AOs
When two #ns# AOs combine with AOs of their own kind, they make #sigma_(ns)# and #sigma_(ns)^"*"# MOs, where #n = 1, 2, 3, ... , N# and #n# is an integer.
The antibonding #sigma_(ns)^"*"# MOs are higher in energy (because they make a node in between where electrons cannot be, thus electrons cannot "shield" as effectively the two nuclei from repelling each other).
The bonding #sigma_(ns)# MOs are lower in energy (otherwise, why bond? Lower energy generally #=># more stable).
FILLING ORBITALS IN THE MO DIAGRAM
Count the number of electrons contributed by each beryllium.
Use the Aufbau principle (fill the orbitals with lowest energy first and go upwards), Hund's Rule (one electron in each orbital of the same energy level at a time, then double up once all orbitals in the same energy level have one electron already), and the Pauli Exclusion Principle (two electrons in the same orbital #=># opposite spins) to fill the orbitals from lowest to highest energy.
Two in the #sigma_(1s)# MO since it is the only one of its specific energy level, then two in the #sigma_(1s)^"*"# MO. Same idea with the #sigma_(2s)# and #sigma_(2s)^"*"# MOs.
CHALLENGE: Can you figure out the MO diagram for #Be_2^(2+)#? How about the electron configuration? Hint: What is the highest-occupied molecular orbital (HOMO)?

