Question #dd444
1 Answer
Explanation:
The most important thing to remember about reactions that take place in multiple steps is that the slowest step is the rate-determining step.
Simply put, the rate of the reaction will depend on the slowest step of the reaction mechanism.
In your case, the overall reaction
#A + B -> C + D#
is said to proceed by the following mechanism
#A + A -> C + E" " " "# slow step
#B + E -> D + A" " " "# fast step
As you can see, adding these two steps will result in the overall reaction. Note that
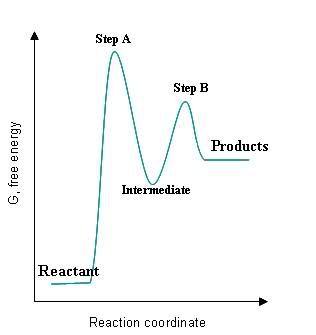
Now, the rate-determining step will be the step with the highest activation energy. A general-form potential energy diagram for a reaction that proceeds in two steps, with the first step being the slow step, looks like this
As you an see, the slow step will have the higher activation energy barrier.
So, the first step in your reaction mechanism is the slow one. In essence, the rate of the reaction will depend on a successful collision between two molecules of
Once a successful collision takes place, the intermediate
This is why the slow step is the rate-determining step.
So, the rate law for the slow step will look like this
#"rate" = k * [A] * [A] = k * [A]^2" "# , where
The rate of the reaction will thus depend on the square of the concentration of reactant
Since the first step is the rate-determining step, doubling the concentration of