Question #f3e7d
1 Answer
Explanation:
The first thing to do here is to determine how many lattice points you get for a face-centered cubic unit cell.
For starters, all three types of cubic lattice unit cells, i.e. simple cubic, body-centered cubic, and face-centered cubic, have lattice points in the corners of the cubic unit cell.
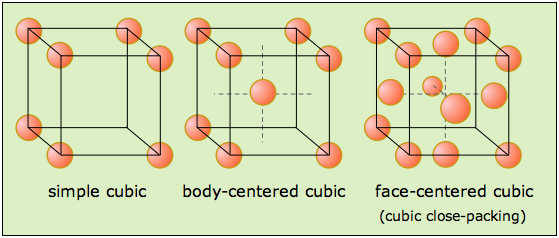
So right from the start you know that the face-centered cubic cell has at least
Now, the characteristic of a face-centered cubic cell is that it also contains lattice points in the centers of the cube's faces.
Since a cube has a total of six faces, it follows that the total number of lattice points you get per unit cell is
#"no. of lattice points" = overbrace("8 lat. pts.")^(color(blue)("corners")) + overbrace("6 lat. pts.")^(color(red)("faces")) = "14 lat. pts."#
To determine the number of atoms that you can fit into a face-centered cubic unit cell, you need to look at how the lattice structure is arranged.
For a given unit cell, pick one of its corners. This corner is being shared by a total of eight unit cells. This means that each corner in a unit cell will contain
Simply put, eight unit cells share one atom per corner.
For a given cell, pick one of its faces. This face is being shared by a total of two unit cells, which means that each face in a unit cell will contain
In other words, two unit cells share one atom per face.
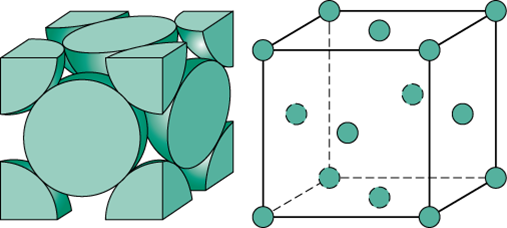
So, the total number of atoms that can fit into a face-centered cubic unit cell will be
#"no. of atoms" = overbrace( 1/8 xx 8)^(color(blue)("8 corners")) + overbrace(1/2 xx 6)^(color(red)("6 faces")) = color(green)("4 atoms")#

